Câu hỏi:

11/10/2024 3,634

Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính \[FA\] (như hình 3).

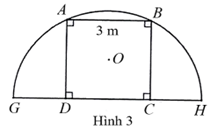
a) Độ dài đoạn thẳng \[OA\] là \(1,5\sqrt 2 \;\,{\rm{m}}\).

b) Độ dài đoạn thẳng \(HG = 3\sqrt 5 \;\,{\rm{m}}\).

c) Độ dài cung \[GAH\] là \(3\sqrt 5 \pi \,\,{\rm{m}}\).

d) Người ta muốn sơn toàn bộ nửa hình tròn (không sơn phần cổng \[ABCD).\] Giá tiền sơn \(30\,\,000\) đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\) Biết \(\pi = 3,14\) kết quả làm tròn đến nghìn đồng. Số tiền sơn là \[1\,\,059\] (nghìn đồng).

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

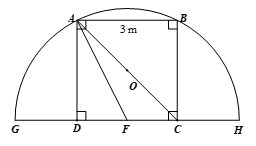
Người ta muốn dựng một khung cổng hình vuông ABCD có độ dài cạnh bằng 3cm được bao bởi một khung thép có dạng nửa đường tròn tâm F bán kínhFA (như hình 3). (ảnh 2)

Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.

a) Ta có \[ABCD\] là hình vuông nên \(\widehat {ABC} = \widehat {ADC} = 90^\circ \) và \(BC = CD = AD = AB = 3{\rm{\;m}}\).

Xét \(\Delta ABC\) vuông tại \(B\), theo định lí Pythagore, ta có:

\(A{C^2} = A{B^2} + A{C^2} = {3^2} + {3^2} = 18.\)

Suy ra \(AC = \sqrt {18} = 3\sqrt 2 {\rm{\;(m)}}{\rm{.}}\)

Do đó \(AO = \frac{1}{2}AC = \frac{1}{2} \cdot 3\sqrt 2 = 1,5\sqrt 2 {\rm{\;(m)}}{\rm{.}}\)

b) Ta có \(F\) là trung điểm của \(CD\) nên \(FD = FC = \frac{1}{2}DC = \frac{1}{2} \cdot 3 = 1,5{\rm{\;(m)}}{\rm{.}}\)

Xét \(\Delta ADF\) vuông tại \(D\), theo định lí Pythagore, ta có:

\(F{A^2} = A{D^2} + D{F^2} = {3^2} + 1,{5^2} = 11,25\).

Suy ra \(FA = \sqrt {11,25} = 1,5\sqrt 5 {\rm{\;(m)}}{\rm{.}}\)

Do đó \(HG = 2FA = 2 \cdot 1,5\sqrt 5 = 3\sqrt 5 {\rm{\;(m)}}{\rm{.}}\)

c) Độ dài cung \[GAH\] là \(\pi \cdot FA = \pi \cdot 1,5\sqrt 5 = 1,5\sqrt 5 \pi {\rm{\;(m)}}{\rm{.}}\)

d) Diện tích cần sơn là \(\frac{1}{2}\pi \cdot F{A^2} - {S_{ABCD}} = \frac{1}{2} \cdot 3,14 \cdot {\left( {1,5\sqrt 5 } \right)^2} - {3^2} = 8,6625{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Số tiền sơn là \(8,6625 \cdot 30\,\,000 \approx 260\,\,000\) (đồng).

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

Huong Pham
11:17 - 31/12/2024

Dữ kiện điểm O là gì ạ? Cho mình biết với được không?

0
Trả lời

Xem thêm ...

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một người đứng trên tháp (tại \(B)\) của ngọn hải đăng cao \[75{\rm{ m}}\] quan sát hai lần một con tàu đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy tàu tại \(C\) với góc hạ là \(20^\circ ,\) lần thứ hai người đó nhìn thấy tàu tại \(D\) với góc hạ là \(30^\circ \) (hình 4). Hỏi con tàu đã đi được bao nhiêu mét giữa hai lần quan sát (Kết quả làm tròn đến hàng đơn vị).

Xem đáp án

Lời giải

Đáp số: \(76{\rm{\;m}}.\)

Ta có \(Bx\) và \(AC\) cùng nằm trên phương ngang nên \(Bx\,{\rm{//}}\,AC,\) do đó \[\widehat {ACB} = \widehat {xBC} = 20^\circ ;\] \(\widehat {ADB} = \widehat {xBD} = 30^\circ \) (các cặp góc so le trong).

Xét tam giác \(ABC\) vuông tại \(A\), ta có \[AC = AB \cdot \cot C = \frac{{AB}}{{\tan C}} = \frac{{75}}{{\tan 20^\circ }}{\rm{\;(m)}}{\rm{.}}\]

Xét tam giác \(ABD\) vuông tại \(A\), ta có \(AD = AB \cdot \cot D = \frac{{AB}}{{\tan D}} = \frac{{75}}{{\tan 30^\circ }}{\rm{\;(m)}}{\rm{.}}\)

Ta có \(CD = AC - AD = \frac{{75}}{{\tan 20^\circ }} - \frac{{75}}{{\tan 30^\circ }} \approx 76{\rm{\;(m)}}{\rm{.}}\)

Vậy con tàu đã đi được xấp xỉ \(76{\rm{\;(m)}}\) giữa hai lần quan sát.

Câu 2

Một trường trung học cơ sở mua 500 quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai \(\left( {x,y \in \mathbb{N}*} \right)\) để làm phần thưởng cho học sinh. Giá bán của mỗi quyển vở loại thứ nhất, loại thứ hai lần lượt là \[8\,\,000\] đồng và \[9\,\,000\] đồng. Biết tổng số tiền nhà trường đã dùng để mua 500 quyển vở đó là \[4\,\,200\,\,000\] đồng. Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; các học sinh khác không được thưởng và số học sinh này chiếm \(40\% \) tổng số học sinh cả trường.

a) \(x + y = 500\).

b) \(9x + 8y = 4\,\,200\,\,000\).

c) \(x = 300;y = 200\).

d) Tổng số học sinh của trường trung học cơ sở đó là 600 học sinh.

Xem đáp án

Lời giải

Đáp án: a) Đúng; b) Sai; c) Đúng; d) Sai.

a) Tổng số quyển vở đã mua là 500 quyển nên \(x + y = 500\).

b) Tổng số tiền nhà trường mua 500 quyển vở là 4 200 000 đồng nên \(8\,\,000x + 9\,\,000y = 4\,\,200\,\,000\) hay \(8x + 9y = 4\,\,200\)

c) Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 500}\\{8x + 9y = 4\,\,200.}\end{array}} \right.\)

Sử dụng máy tính cầm tay giải hệ phương trình (1) ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 300}\\{y = 200}\end{array}} \right.\) (thỏa mãn điều kiện).

d) Gọi \(u,\,\,v\) lần lượt là số học sinh Xuất sắc và số học sinh Giỏi \(\left( {u,\,\,v \in {\mathbb{N}^*}} \right)\).

Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai nên ta có phương trình \(2u + v = 300.\)

Mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai nên ta có phương trình \(u + v = 200.\)

Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2u + v = 300}\\{u + v = 200}\end{array}} \right.\) (2).

Sử dụng máy tính cầm tay giải hệ phương trình (2) ta được \(\left\{ {\begin{array}{*{20}{l}}{u = 100}\\{v = 100}\end{array}} \right.\) (thỏa mãn điều kiện).

Vậy có tổng \(100 + 100 = 200\) học sinh Xuất sắc và Giỏi, chiếm \(40\% \) tổng số học sinh cả trường.

Do đó, tổng số học sinh của trường là \(200:40\% = 500\) (học sinh).

Câu 3