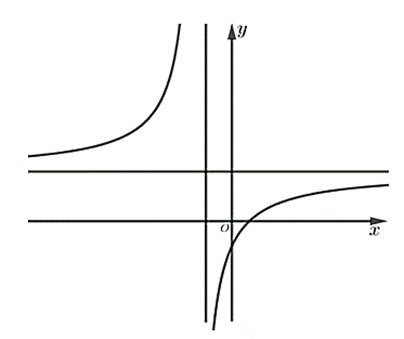
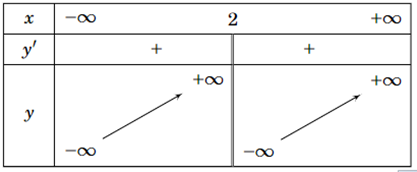
Bảng biến thiên sau là của đồ thị hàm số nào
A. \(y = \frac{{{x^2} - 3}}{{x - 2}}\).
B. \(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
C. \(y = \frac{{{x^2} - x}}{{x - 2}}\).
D. \(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Dựa vào bảng biến thiên ta có đồ thị hàm số có tiệm cận đứng x = 2 và hàm số đồng biến trên khoảng (−∞; 2) và (2; +∞).
+) Xét hàm số\(y = \frac{{{x^2} - 3}}{{x - 2}}\) có \(y' = \frac{{2x\left( {x - 2} \right) - \left( {{x^2} - 3} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
+) Xét hàm số \(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\) có:
\(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 2} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 6}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{{\left( {x - 2} \right)}^2} + 2}}{{{{\left( {x - 2} \right)}^2}}} > 0\). Chọn.
+) Xét hàm số \(y = \frac{{{x^2} - x}}{{x - 2}}\) có \(y' = \frac{{\left( {2x - 1} \right)\left( {x - 1} \right) - \left( {{x^2} - x} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 2x + 1}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
+) Xét hàm số \(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\) có:
\(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 5} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(x = 5{\rm{ (cm)}}{\rm{.}}\)
B. \(x = 9{\rm{ (cm)}}{\rm{.}}\)
C. \(x = 8{\rm{ (cm)}}{\rm{.}}\)
D. \(x = 10{\rm{ (cm)}}{\rm{.}}\)
Lời giải
Đáp án đúng là: D
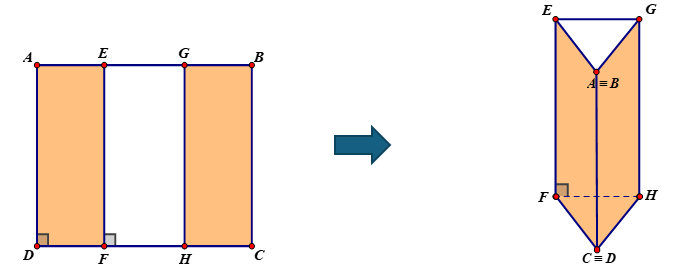
Gọi \(p\) là nửa chu vi tam giác \(DHF\).
Ta có: \(DF = CH = x,{\rm{ }}FH = 30 - 2x \Rightarrow p = 15.\)
Thể tích khối lăng trụ như hình vẽ là
\(V = {S_{\Delta FDH}}.EF = 30\sqrt {15(15 - x)(15 - x)(15 - 30 + 2x)} \)\( = 30\sqrt {15{{(15 - x)}^2}(2x - 15)} .\)
Xét hàm số \(f(x) = {(15 - x)^2}(2x - 15)\),\(x \in \left( {\frac{{15}}{2};15} \right)\).
\[f'(x) = - 2(15 - x)(2x - 15) + 2{(15 - x)^2} = - 2(15 - x)(3x - 30)\]; \(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\left( {TM} \right)\\x = 15\left( {KTM} \right)\end{array} \right.\).
Bảng biến thiên:
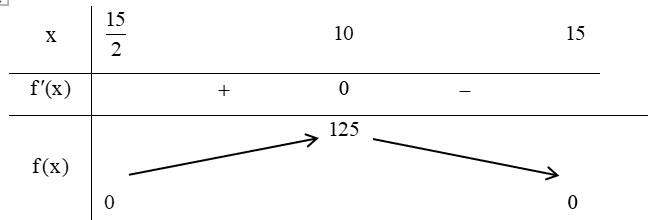
Dựa vào bảng biến thiên, ta thấy: \(\mathop {\max }\limits_{\left( {\frac{{15}}{2};15} \right)} f(x) = 125\) khi \(x = 10.\)
Do đó thể tích khối lăng trụ như hình vẽ lớn nhất: \({V_{\max }} = 750\sqrt 3 {\rm{ (c}}{{\rm{m}}^3}).\) Khi đó: \(x = 10{\rm{ (cm)}}{\rm{.}}\)
Câu 2
A. \(y = \frac{{{x^2} - 3x + 4}}{{ - x - 4}}\).
B. \(y = \frac{{{x^2} - 4x + 4}}{{ - x - 4}}\).
C. \(y = \frac{{{x^2} - 5x + 4}}{{x + 4}}\).
D. \(y = \frac{{{x^2} - 4x + 4}}{{x + 4}}\).
Lời giải
Đáp án đúng là: B
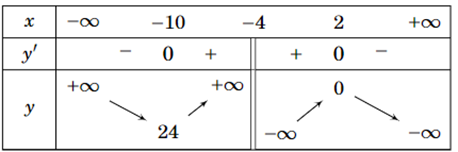
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng là x = −4.
Đồ thị hàm số đi qua hai điểm (−10; 24) và (2; 0) nên thay tọa độ 2 điểm vào các hàm số ta thấy đáp án B thỏa mãn.
Câu 3
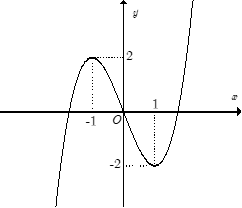
A. y = x3 – 3x.
B. y = −x3 + 3x.
C. y = −x4 + 2x2.
D. y = x4 − 2x2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
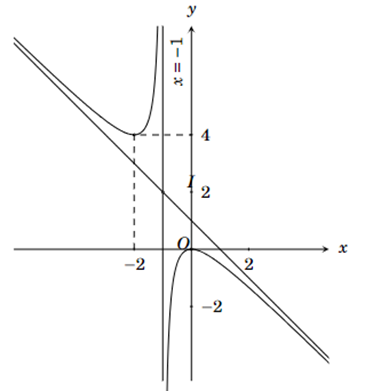
A. \(y = \frac{{{x^2} - x}}{{x + 1}}\).
B. \(y = \frac{{{x^2} - 3x}}{{x + 1}}\).
C. \(y = \frac{{{x^2} + x + 2}}{{x + 1}}\).
D. \(y = \frac{{ - {x^2}}}{{x + 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. a < 0, b > 0, c > 0, d < 0.
B. a < 0, b < 0, c > 0, d
C. a > 0, b < 0, c < 0, d > 0
D. a < 0, b > 0, c < 0, d < 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[1,08\] triệu đồng.
B. \[0,91\] triệu đồng.
C. \[1,68\] triệu đồng.
D. \[0,54\] triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. y = −x3 + 3x2 + 9x – 2.
B. \(y = \frac{1}{3}{x^3} - {x^2} - 3x - \frac{2}{3}\) .
C. y = x3 − 3x2 − 9x – 2.
D. \(y = - \frac{1}{3}{x^3} + {x^2} + 3x + \frac{2}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo