Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d.\] Chọn khẳng định đúng?
A. \[d > R + r.\]
Quảng cáo
Trả lời:
Đáp án đúng là: D
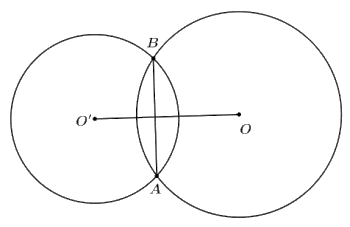
Ta thấy hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau khi \[R - r < d < R + r\] với \[R > r.\] </>
Do đó ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[4{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: C

Kẻ \[OH \bot AB\] tại \[H.\]
Vì khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}\] nên ta có \[OH = 3{\rm{\;cm}}.\]
Áp dụng định lí Pythagore cho tam giác \[OHB\] vuông tại \[H,\] ta được: \[O{H^2} + H{B^2} = O{B^2}.\]
Suy ra \[H{B^2} = O{B^2} - O{H^2} = {R^2} - O{H^2} = {5^2} - {3^2} = 16\]. Do đó \[HB = 4{\rm{\;(cm)}}{\rm{.}}\]
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R\]) có \[OH\] là đường cao nên \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Suy ra \[AB = 2 \cdot HB = 2 \cdot 4 = 8{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án B.
Câu 2
A. \[2 + \sqrt {11} {\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Đáp án đúng là: C
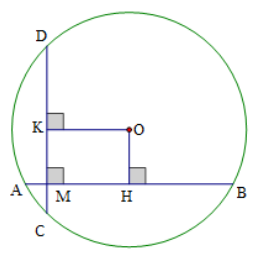
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R)\] có \[OH\] là đường cao nên \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Vì vậy \[HA = HB = \frac{{AB}}{2} = \frac{{16}}{2} = 8{\rm{\;(cm)}}{\rm{.}}\]
Chứng minh tương tự, ta được \[KC = KD = \frac{{CD}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[KC = KM + MC.\] Suy ra \[KM = KC - MC = 6 - 2 = 4{\rm{\;(cm)}}{\rm{.}}\]
Tứ giác \[OHMK\] có: \[\widehat {OKM} = \widehat {KMH} = \widehat {OHM} = 90^\circ \] nên tứ giác \[OHMK\] là hình chữ nhật.
Do đó \[OH = KM = 4{\rm{\;(cm)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác \[OHB\] vuông tại \[H,\] ta được:
\[O{B^2} = O{H^2} + H{B^2} = {4^2} + {8^2} = 80\]. Suy ra \[R = OB = 4\sqrt 5 {\rm{\;(cm)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác \[OKD\] vuông tại \[K,\] ta được: \[O{D^2} = O{K^2} + K{D^2}.\]
Suy ra \[O{K^2} = O{D^2} - K{D^2} = {R^2} - K{D^2} = {\left( {4\sqrt 5 } \right)^2} - {6^2} = 44\]
Do đó \[OK = 2\sqrt {11} {\rm{\;(cm)}}{\rm{.}}\]
Vậy diện tích hình chữ nhật \[OHMK\] là: \[S = KM \cdot OK = 4 \cdot 2\sqrt {11} = 8\sqrt {11} {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Do đó ta chọn phương án C.
Câu 3
A. tiếp xúc trong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(1{\rm{\;cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng.
C. Đường tròn có hai trục đối xứng là hai đường thẳng đi qua tâm và vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2{\rm{\;cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[38{\rm{\;m}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.