Cho đường tròn \(\left( O \right)\) đi qua ba điểm \(A,\,\,B,\,\,C\). Biết \(\widehat {ACB} = 56^\circ ,\) số đo của cung nhỏ \(AB\) là
A. \(28^\circ \).
B. \(56^\circ \).
C. \(112^\circ \).
D. \(248^\circ \).
Quảng cáo
Trả lời:
Đáp án đúng là: C
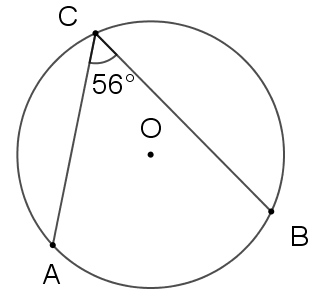
Xét đường tròn \(\left( O \right)\) ta có \[\widehat {ACB},\,\,\widehat {AOB}\] lần lượt là góc nội tiếp và góc ở tâm chắn cung nhỏ \[AB\].
Do đó \[\widehat {AOB} = 2\widehat {ACB} = 2 \cdot 56^\circ = 112^\circ .\] hay
Vậy số đo của cung nhỏ \[AB\] là: O10-2024-GV154
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(60^\circ \).
B. \(80^\circ \).
C. \(120^\circ \).
D. \(150^\circ \).
Lời giải
Đáp án đúng là: C
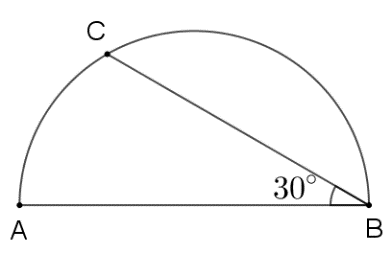
Vì \[\widehat {ABC}\] là góc nội tiếp chắn cung \(AC\) nên ta có
Số đo của nửa đường tròn là
Số đo của cung \[BC\] là:
Câu 2
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
Lời giải
Đáp án đúng là: B
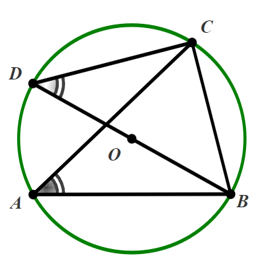
Đường tròn \[\left( O \right)\] có \[\widehat {CDB}\] và \[\widehat {CAB}\] là hai góc nội tiếp cùng chắn cung \[CB\] nên \(\widehat {CDB} = \widehat {CAB} = 45^\circ \).
Do \[\widehat {DCB}\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {DCB} = 90^\circ \).
Xét \(\Delta DCB\) có: \(\widehat {CBD} + \widehat {CDB} + \widehat {DCB} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {CBD} = 180^\circ - \widehat {CDB} - \widehat {DCB} = 180^\circ - 45^\circ - 90^\circ = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
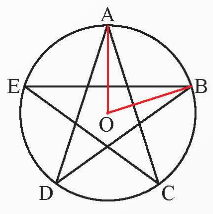
A. \[72^\circ .\]
B. \[288^\circ .\]
C. \[60^\circ .\]
D. \[300^\circ .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.