Cho tam giác nhọn \[ABC\] có ba đỉnh nằm trên đường tròn \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\] và gọi\[M\] là trung điểm \[BC\]. Cho các khẳng định sau:
(i) \(OM \bot BC\).
(ii) \(OM\,{\rm{//}}\,AH\).
(iii) \(HM = \frac{{HF}}{2}\).
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 0.
B. 1.
C. 2.
D. 3.
Quảng cáo
Trả lời:
Đáp án đúng là: D
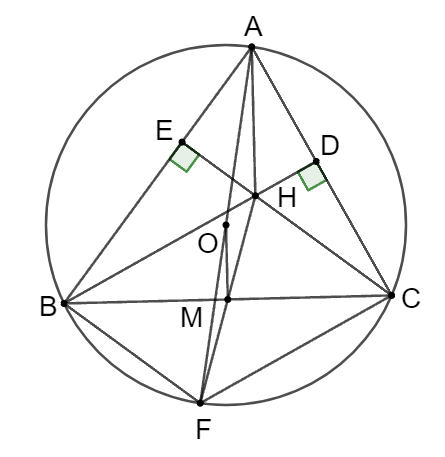
⦁ Xét đường tròn \[\left( O \right)\] có \(\widehat {ABF} = 90^\circ \) và \(\widehat {ACF} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn)
Suy ra \[BF \bot \;AB\] và \[CF \bot \;AC\]
Mà \[CE \bot \;AB\] và \[BD \bot \;AC\] nên \[CE\,{\rm{//}}\,BF,\] \[BD\,{\rm{//}}\,CF\].
Suy ra \[BHCF\] là hình bình hành, do đó hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lại có \[M\] là trung điểm của \[BC\] nên \[M\] cũng là trung điểm của \[HF\] hay \(HM = \frac{{HF}}{2}\).
⦁ Xét \(\Delta AHF\) có \(O,\,\,M\) lần lượt là trung điểm của \(AF,\,\,HF\) nên \[OM\] là đường trung bình của tam giác \[AHF\], do đó \[AH\,{\rm{//}}\,OM\].
⦁ Xét tam giác \[ABC\] có \[BD\] và \[CE\] là hai đường cao cắt nhau tại \[H\] nên \[H\] là trực tâm tam giác \[ABC\]. Suy ra \[AH \bot \;BC\] mà \[AH\,{\rm{//}}\,OM\], do đó \[OM \bot \;BC\].
Vậy cả ba khẳng định đã cho đều đúng, ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(60^\circ \).
B. \(80^\circ \).
C. \(120^\circ \).
D. \(150^\circ \).
Lời giải
Đáp án đúng là: C
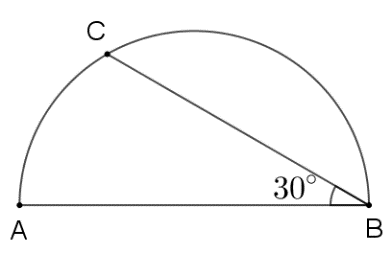
Vì \[\widehat {ABC}\] là góc nội tiếp chắn cung \(AC\) nên ta có
Số đo của nửa đường tròn là
Số đo của cung \[BC\] là:
Câu 2
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
Lời giải
Đáp án đúng là: B
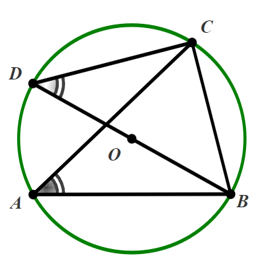
Đường tròn \[\left( O \right)\] có \[\widehat {CDB}\] và \[\widehat {CAB}\] là hai góc nội tiếp cùng chắn cung \[CB\] nên \(\widehat {CDB} = \widehat {CAB} = 45^\circ \).
Do \[\widehat {DCB}\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {DCB} = 90^\circ \).
Xét \(\Delta DCB\) có: \(\widehat {CBD} + \widehat {CDB} + \widehat {DCB} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {CBD} = 180^\circ - \widehat {CDB} - \widehat {DCB} = 180^\circ - 45^\circ - 90^\circ = 45^\circ \).
Câu 3
A. \(28^\circ \).
B. \(56^\circ \).
C. \(112^\circ \).
D. \(248^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
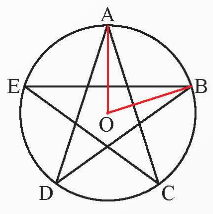
Câu 5
A. \[72^\circ .\]
B. \[288^\circ .\]
C. \[60^\circ .\]
D. \[300^\circ .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.