Cho nửa đường tròn 
và đường kính 
. Từ 
và 
kẻ hai tiếp tuyến 
. Qua điểm 
thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến lần lượt ở 
và 
. Các đường thẳng 
và 
cắt nhau tại 
.
Cho 
. Tính diện tích hình quạt giới hạn bởi các bán kính 
và cung nhỏ 
Cho nửa đường tròn và đường kính . Từ và kẻ hai tiếp tuyến . Qua điểm thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến lần lượt ở và . Các đường thẳng và cắt nhau tại .
Cho và đường kính . Từ và kẻ hai tiếp tuyến . Qua điểm thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến lần lượt ở và . Các đường thẳng và cắt nhau tại .. Tính diện tích hình quạt giới hạn bởi các bán kính và cung nhỏ Quảng cáo
Trả lời:
Giải bởi Vietjack
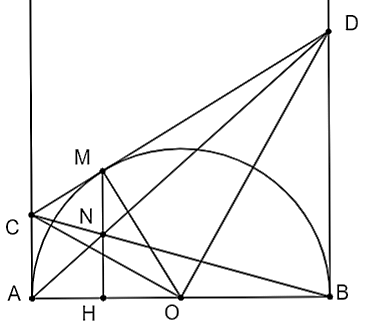
Xét tam giác \[MOD\], có: \[\cos \widehat {MOD} = \frac{{MO}}{{OD}} = \frac{{MO}}{{2MO}} = \frac{1}{2}\], suy ra \[\widehat {MOD} = 60^\circ \].
Theo câu a, \[OD\] là tia phân giác của \[\widehat {BOM}\] nên \[\widehat {BOM} = 2\widehat {MOD} = 2 \cdot 60^\circ = 120^\circ .\]
Mà \[\widehat {AOM} + \widehat {BOM} = 180^\circ \] (câu a)
Suy ra \[\widehat {AOM} = 180^\circ - \widehat {BOM} = 180^\circ - 120^\circ = 60^\circ \].
Mà \(\widehat {AOM}\) là góc ở tâm chắn cung \(AM\) nhỏ nên
Diện tích hình quạt giới hạn bởi bán kính \[OM,\,\,OA\] và cung nhỏ \[MA\] là:
\[S = \frac{{60 \cdot \pi \cdot {R^2}}}{{360}} = \frac{{\pi {R^2}}}{6}\] (đơn vị diện tích).
Vậy diện tích hình quạt giới hạn bởi các bán kính \[OM,\,\,OA\] và cung nhỏ \[MA\] là \[\frac{{\pi {R^2}}}{6}\] (đvdt).Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét tam giác 
vuông tại 
, ta có:
Xét tam giác 
vuông tại , ta có:
Do 
nên 
Hay 
.
Suy ra 
(m).
Vậy tháp Eiffel có độ cao khoảng 
(m).
Lời giải
Chiều dài của đáy bể là 
Diện tích đáy của bể là 
Chiều cao của bể là: 
.
Diện tích xung quanh của bể là: 
Diện tích cần xây bằng tổng diện tích xung quanh và diện tích đáy của bể, và bằng:
Do 
là chiều rộng của bể nên 
, áp dụng bất đẳng thức Cauchy, ta có:
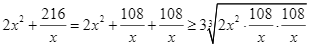
Suy ra 
Dấu “=” xảy ra khi 
hay 
, tức là 
Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập