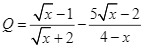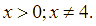Phương trình \[\frac{3}{{x + 1}} + \frac{5}{{x - 2}} = \frac{{5x + 8}}{{\left( {x - 2} \right)\left( {x + 1} \right)}}\] có nghiệm \[x = a\]. Tìm \[a.\]
Phương trình \[\frac{3}{{x + 1}} + \frac{5}{{x - 2}} = \frac{{5x + 8}}{{\left( {x - 2} \right)\left( {x + 1} \right)}}\] có nghiệm \[x = a\]. Tìm \[a.\]
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án: \[3\]
Điều kiện xác định của phương trình là: \[x \ne - 1,x \ne 2.\]
Ta có: \[\frac{3}{{x + 1}} + \frac{5}{{x - 2}} = \frac{{5x + 8}}{{\left( {x - 2} \right)\left( {x + 1} \right)}}\]
\[\frac{{3\left( {x - 2} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} + \frac{{5\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{{5x + 8}}{{\left( {x - 2} \right)\left( {x + 1} \right)}}.\]
\[3\left( {x - 2} \right) + 5\left( {x + 1} \right) = 5x + 8\]
\[3x - 6 + 5x + 5 = 5x + 8\]
\[3x = 9\]
\[x = 3\] (TM).
Mà \[x = a\] nên \[a = 3.\]
Vậy để phương trình đã cho có nghiệm \[x = a\] thì \[a = 3.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: 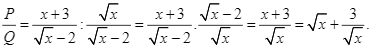
Vì 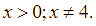 nên
nên 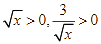 .
.
Áp dụng bất đẳng thức Cauchy cho hai số không âm ![]() ta được:
ta được:
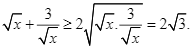
Suy ra ![]()
Dấu “=” xảy ra khi ![]() hay
hay ![]() (TMĐK).
(TMĐK).
Vậy giá trị nhỏ nhất của ![]() khi
khi ![]()
Lời giải
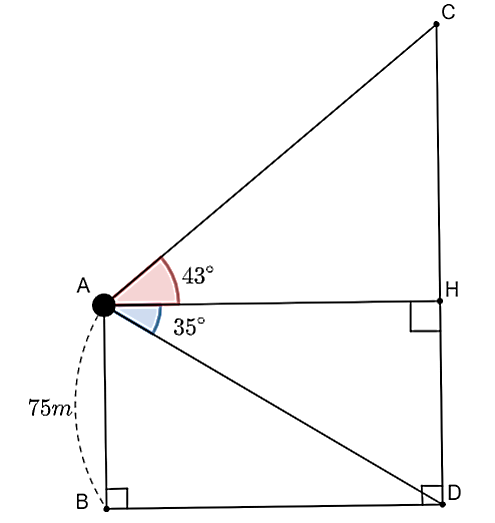
Ta có: \[\widehat {ABD} = \widehat {BDH} = \widehat {DHA} = 90^\circ \] nên tứ giác \[AHDC\] là hình chữ nhật.
Do đó, \[AB = DH = 75{\rm{ m}}{\rm{.}}\]
Xét tam giác vuông \[DHA\], có: \[\tan \widehat {HAD} = \frac{{HD}}{{HA}}\] suy ra \[AH = \frac{{HD}}{{\tan \widehat {HAD}}} = \frac{{75}}{{\tan 35^\circ }}{\rm{ }}\left( {\rm{m}} \right).\]
Xét tam giác vuông \[AHC\], có: \[CH = AH.\tan \widehat {CAH} = \frac{{75}}{{\tan 35^\circ }}.\tan 43^\circ \approx 99,88{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Do đó, chiều cao \[CD\] là: \[CD = DH + CH \approx 75 + 99,88 = 174,88{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Vậy chiều cao của trạm phát sóng đó khoảng \[174,88{\rm{ m}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.