Câu hỏi:
23/12/2024 92
Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s2. Cùng lúc đó, một ô tô đang chạy với vận tốc 20 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s2. Biết dốc dài 570 m.
a) Xác định vị trí hai xe gặp nhau trên dốc.
b) Tính vận tốc của xe đạp ở dưới chân dốc.
Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s2. Cùng lúc đó, một ô tô đang chạy với vận tốc 20 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s2. Biết dốc dài 570 m.
a) Xác định vị trí hai xe gặp nhau trên dốc.
b) Tính vận tốc của xe đạp ở dưới chân dốc.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Quãng đường xe đạp đi được đến khi hai xe gặp nhau là:\[{s_1} = {v_{01}}t + \frac{1}{2}{a_1}{t^2} = 2.t + \frac{1}{2}.0,2.{t^2}\]
Quãng đường ô tô đi được đến khi hai xe gặp nhau là: \[{s_2} = {v_{02}}t + \frac{1}{2}{a_2}{t^2} = 20.t + \frac{1}{2}.\left( { - 0,4} \right).{t^2}\]
Ta có: \[{s_1} + {s_2} = 570 \Rightarrow 2t + \frac{1}{2}.0,2.{t^2} + 20t + \frac{1}{2}.\left( { - 0,4} \right){t^2} = 570\]
\[ \Rightarrow - 0,1{t^2} + 22t - 570 = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{t = 190s}\\{t = 30s}\end{array}} \right.\]
Thay \[t = 190s\] vào \[{s_1}\] ta được: \[{s_1} = 3990 > 570\] (Loại)
Thay \[t = 30s\] vào \[{s_1}\] ta được: \[{s_1} = 150 < 570\] (Thỏa mãn)
Vậy hai xe gặp nhau tại vị trí cách đỉnh dốc 150 m.
b) Vận tốc của xe dưới chân dốc là
\[v_1^2 - v_{01}^2 = 2.{a_1}.s \Rightarrow {v_1} = \sqrt {v_{01}^2 + 2{a_1}.s} = \sqrt {{2^2} + 2.0,2.570} = 2\sqrt {58} \left( {m/s} \right)\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vận tốc của vật khi chạm đất là: \[{v^2} - v_0^2 = 2gH \Rightarrow v = \sqrt {2gH} = \sqrt {2.9,8.19,6} = 19,6\left( {m/s} \right)\]
b) Thời gian rơi của vật là: \[t = \sqrt {\frac{{2H}}{g}} = \sqrt {\frac{{2.19,6}}{{9,8}}} = 2\left( s \right)\]
c) Quãng đường vật đi được trong một giây đầu tiên là: \[s = \frac{1}{2}g{t^2} = \frac{1}{2}.9,{8.1^2} = 4,9\left( m \right)\]
Quãng đường vật đi được trong một giây cuối cùng là: \[s' = 19,6 - 4,9 = 14,7\left( m \right)\]
Lời giải
a. Vẽ đồ thị
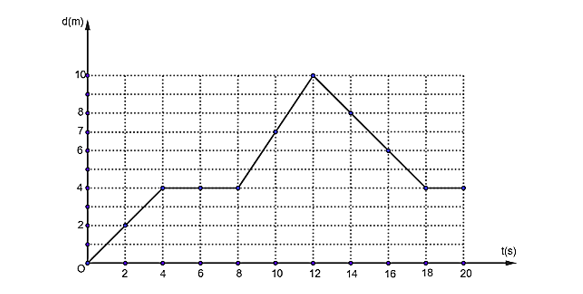
b. Vận tốc tức thời tại:
+ t = 6s: \(v = 0\,\)
+ t = 10s: \(v = \frac{{7 - 4}}{{10 - 8}} = 1,5\,m/s\)
+ t = 16s: \(v = \frac{d}{t} = \frac{{6 - 10}}{{16 - 12}} = - 1\,m/s\)
![Hai vật \[A\] và \[B\] chuyển động cùng chiều trên một đường thẳng có đồ thị vận tốc – thời gian (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/12/blobid4-1734941753.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận