Câu hỏi:
23/12/2024 186
Một viên đạn được bắn theo phương nằm ngang từ một khẩu súng đặt ở độ cao 45,0 m so với mặt đất. Vận tốc của viên đạn khi vừa ra khỏi nòng súng có độ lớn là 250 m/s. Lấy g = 9,8 m/s2.
a) Sau bao lâu thì viên đạn chạm đất?
b) Viên đạn rơi xuống đất cách điểm bắn theo phương nằm ngang bao nhiêu mét?
c) Ngay trước khi chạm đất, vận tốc của viên đạn có độ lớn bằng bao nhiêu?
Một viên đạn được bắn theo phương nằm ngang từ một khẩu súng đặt ở độ cao 45,0 m so với mặt đất. Vận tốc của viên đạn khi vừa ra khỏi nòng súng có độ lớn là 250 m/s. Lấy g = 9,8 m/s2.
a) Sau bao lâu thì viên đạn chạm đất?
b) Viên đạn rơi xuống đất cách điểm bắn theo phương nằm ngang bao nhiêu mét?
c) Ngay trước khi chạm đất, vận tốc của viên đạn có độ lớn bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Thời gian từ lúc bắt đầu chuyển động đến khi chạm đất của viên đạn:
\(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.45}}{{9,8}}} = 3,03s\).
b) Tầm xa: \(L = {v_0}t = 250.3,03 = 757,5\,m\)
c) Vận tốc của viên đạn khi chạm đất có 2 thành phần:
Thành phần theo phương thẳng đứng: \({v_y} = gt = 9,8.3,03 = 29,7m/s\)
Thành phần theo phương ngang: \[{v_x} = {v_0} = 250\,m/s\]
Vận tốc khi chạm đất: \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {29,{7^2} + {{250}^2}} \approx 252m/s\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vận tốc của vật khi chạm đất là: \[{v^2} - v_0^2 = 2gH \Rightarrow v = \sqrt {2gH} = \sqrt {2.9,8.19,6} = 19,6\left( {m/s} \right)\]
b) Thời gian rơi của vật là: \[t = \sqrt {\frac{{2H}}{g}} = \sqrt {\frac{{2.19,6}}{{9,8}}} = 2\left( s \right)\]
c) Quãng đường vật đi được trong một giây đầu tiên là: \[s = \frac{1}{2}g{t^2} = \frac{1}{2}.9,{8.1^2} = 4,9\left( m \right)\]
Quãng đường vật đi được trong một giây cuối cùng là: \[s' = 19,6 - 4,9 = 14,7\left( m \right)\]
Lời giải
a. Vẽ đồ thị
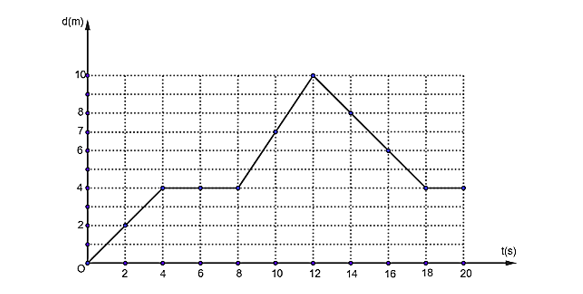
b. Vận tốc tức thời tại:
+ t = 6s: \(v = 0\,\)
+ t = 10s: \(v = \frac{{7 - 4}}{{10 - 8}} = 1,5\,m/s\)
+ t = 16s: \(v = \frac{d}{t} = \frac{{6 - 10}}{{16 - 12}} = - 1\,m/s\)
![Hai vật \[A\] và \[B\] chuyển động cùng chiều trên một đường thẳng có đồ thị vận tốc – thời gian (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/12/blobid4-1734941753.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án