Vật nhỏ nặng 100 g gắn với một lò xo nhẹ đang dao động điều hoà dọc theo một trục nằm trong mặt phẳng ngang trên đệm không khí có li độ \(x = \sqrt 2 {\rm{sin}}\left( {100\pi t - \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right).\) Nếu tắt đệm không khí, độ giảm cơ năng của vật đến khi vật hoàn toàn dừng lại là bao nhiêu?
Vật nhỏ nặng 100 g gắn với một lò xo nhẹ đang dao động điều hoà dọc theo một trục nằm trong mặt phẳng ngang trên đệm không khí có li độ \(x = \sqrt 2 {\rm{sin}}\left( {100\pi t - \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right).\) Nếu tắt đệm không khí, độ giảm cơ năng của vật đến khi vật hoàn toàn dừng lại là bao nhiêu?
Câu hỏi trong đề: 14 bài tập Chủ đề 1. Dao động có lời giải !!
Quảng cáo
Trả lời:
Độ giảm cơ năng của vật đến khi vật hoàn toàn dừng lại là:
\({\rm{\Delta }}W = W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,1.{(100\pi )^2}.{\left( {\sqrt 2 {{.10}^{ - 2}}} \right)^2} \approx 1{\rm{\;J}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
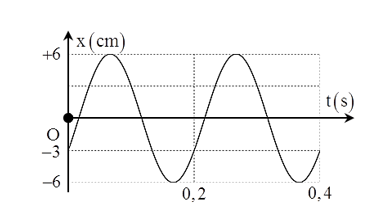
Tần số góc: \[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi \,\,rad/s\]
a) Biên độ \(A = \frac{{{\ell _{\max }} - {\ell _{\min }}}}{2} = \frac{{0,24 - 0,2}}{2} = 0,02\;{\rm{m}}\)
b) Tốc độ cực đại: \({v_{\max }} = \omega A = 5\pi .0,02 = 0,3\;{\rm{m/s}}\)
Gia tốc cực đại: \({a_{\max }} = {\omega ^2}A = {\left( {5\pi } \right)^2}.0,02 = 5{\rm{\;m/}}{{\rm{s}}^{\rm{2}}}\)
c) Độ cứng của lò xo: \(k = \frac{{4{\pi ^2}m}}{{{T^2}}} = \frac{{4{\pi ^2}.0,2}}{{0,{4^2}}} = 49{\rm{\;N/m}}\)
Độ dãn của lò xo khi vật ở vị trí cân bằng là: \(\Delta {\ell _0} = \frac{{mg}}{k} = \frac{{0,2.9,8}}{{49}} = 0,04\;{\rm{m}}\)
Chiều dài của lò xo khi chưa biến dạng: \(\Delta {\ell _{\max }} = A + \Delta {\ell _0} = 0,02\; + 0,04\; = 0,06\;{\rm{m}}{\rm{.}}\)
Câu 2
A. \(x = 4\cos \left( {4\pi t + \frac{{5\pi }}{3}} \right)\,cm.\)
B. \(x = 4\cos \left( {4\pi t - \frac{\pi }{3}} \right)\,cm.\)
Lời giải
Tần số góc: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,25}} = 8\pi \left( {rad/s} \right).\)
Tại thời điểm ban đầu:
\(\left\{ \begin{array}{l}x < 0\\v = 16\pi \,\left( {cm/s} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\cos \varphi < 0\\ - \omega A\sin \varphi = 16\pi \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi < 0\\\sin \varphi = \frac{{16\pi }}{{ - 8\pi .4}} = - \frac{1}{2}\end{array} \right. \Rightarrow \varphi = - \frac{{5\pi }}{6}\left( {rad} \right).\)
Phương trình dao động: \(x = 4\cos \left( {8\pi t - \frac{{5\pi }}{6}} \right)\,cm.\) Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(v = 30\pi \cos \left( {5\pi t - \frac{\pi }{6}} \right)\)cm/s.
B. \(v = 60\pi \cos \left( {10\pi t - \frac{\pi }{3}} \right)\)cm/s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.