Trong vật lí, quãng đường S (tính bằng mét) của một vật rơi tự do được cho bởi công thức S = 4,9t2, trong đó l là tời gian rơi (tính bằng giây). Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?
A. 5s.
B. 15s.
C. 25s.
D. 20s.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Từ công thức S = 4,9t2 suy ra t2 = \(\frac{S}{{4,9}}\), suy ra t = \(\sqrt {\frac{S}{{4,9}}} \) (vì t > 0).
Vật đang ở độ cao 122,5 m rơi chạm đất thì vật đã rơi được quãng đường là
S = 122,5 m.
Thay S = 122,5 m vào phương trình t = \(\sqrt {\frac{S}{{4,9}}} = \sqrt {\frac{{122,5}}{{4,9}}} = 5(s)\).
Vậy sau 5 s thì vật rơi chạm đất.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
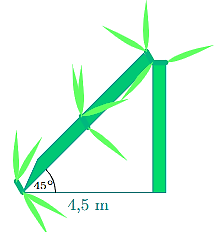
A. 4,5 m.
B. 10,9 m.
C. 19 m.
D. 9 m.
Lời giải
Đáp án đúng là: B
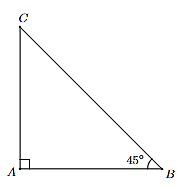
Xem đoạn bị gãy là CB, đoạn còn lại (thẳng đứng) là AC.
Như vậy, độ dài của cây khi chưa bị gãy là AC + BC.
Do tam giác ABC vuông tại A và \(\widehat {ABC}\) = 45°, suy ra tam giác ABC vuông cân tại A.
Suy ra AC = AB = 4,5 m.
Áp dụng định lí Pythagore trong tam giác ABC, ta có:
AB2 + AC2 = BC2
4,52 + 4,52 = BC2
Suy ra BC = \(\sqrt {2.4,{5^2}} = \sqrt {40,5} \) m.
Vậy chiều cao cây trước khi gãy là: 4,5 + \(\sqrt {40,5} \) ≈ 10,9 m.
Câu 2
A. 23,03 m.
B. 23,3 m.
C. 230,3 m.
D. 203 m.
Lời giải
Đáp án đúng là: C
Gọi cạnh hình vuông (nền kim tự tháp) là x, điều kiện x > 0, đơn vị m.
Diện tích hình vuông là: x2 = 53 052.
Suy ra x = \(\sqrt {53052} \) ≈ 230,3 m.
Vậy độ dài cạnh nền của kim tự tháp khoảng 230,3 m.
Câu 3
A. \[\sqrt {{{500}^2} + {x^2}} \] + \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
B. \[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
C. \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \] − \[\sqrt {{{500}^2} + {x^2}} \].
D. −\[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 1 404 m.
B. 1 044 m.
C. 1 400 m.
D. 1 440 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập