Trong một thí nghiệm, một vật rơi tự do từ độ cao 80 m so với mặt đất. Biết rằng quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức h = 5t2 với t là thời gian vật đó rơi, tính theo đơn vị giây
(t > 0). Hỏi sau bao nhiêu lâu kể từ lúc rơi thì vật đó chạm đất?
Trong một thí nghiệm, một vật rơi tự do từ độ cao 80 m so với mặt đất. Biết rằng quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức h = 5t2 với t là thời gian vật đó rơi, tính theo đơn vị giây
(t > 0). Hỏi sau bao nhiêu lâu kể từ lúc rơi thì vật đó chạm đất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi vật chạm đất thì quãng đường dịch chuyển được của vật đó là 80 m.
Ta có: 80 = 5t2 hay t2 = 16.
Do đó, t = \(\sqrt {16} \) = 4 hoặc t = \( - \sqrt {16} \) = −4.
Mà t > 0 nên t = 4.
Vậy sau 4 giây kể từ lúc tơi thì vật đó chạm đất.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
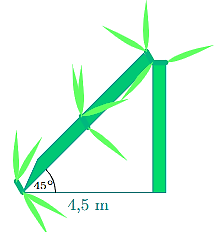
A. 4,5 m.
B. 10,9 m.
C. 19 m.
D. 9 m.
Lời giải
Đáp án đúng là: B
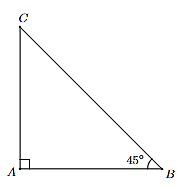
Xem đoạn bị gãy là CB, đoạn còn lại (thẳng đứng) là AC.
Như vậy, độ dài của cây khi chưa bị gãy là AC + BC.
Do tam giác ABC vuông tại A và \(\widehat {ABC}\) = 45°, suy ra tam giác ABC vuông cân tại A.
Suy ra AC = AB = 4,5 m.
Áp dụng định lí Pythagore trong tam giác ABC, ta có:
AB2 + AC2 = BC2
4,52 + 4,52 = BC2
Suy ra BC = \(\sqrt {2.4,{5^2}} = \sqrt {40,5} \) m.
Vậy chiều cao cây trước khi gãy là: 4,5 + \(\sqrt {40,5} \) ≈ 10,9 m.
Lời giải
Đáp án đúng là: A
Từ công thức S = 4,9t2 suy ra t2 = \(\frac{S}{{4,9}}\), suy ra t = \(\sqrt {\frac{S}{{4,9}}} \) (vì t > 0).
Vật đang ở độ cao 122,5 m rơi chạm đất thì vật đã rơi được quãng đường là
S = 122,5 m.
Thay S = 122,5 m vào phương trình t = \(\sqrt {\frac{S}{{4,9}}} = \sqrt {\frac{{122,5}}{{4,9}}} = 5(s)\).
Vậy sau 5 s thì vật rơi chạm đất.
Câu 3
A. 23,03 m.
B. 23,3 m.
C. 230,3 m.
D. 203 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 1 404 m.
B. 1 044 m.
C. 1 400 m.
D. 1 440 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\sqrt {{{500}^2} + {x^2}} \] + \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
B. \[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
C. \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \] − \[\sqrt {{{500}^2} + {x^2}} \].
D. −\[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo