Sử dụng dữ kiện bài toán dưới đây để trả lời Bài 7, 8.
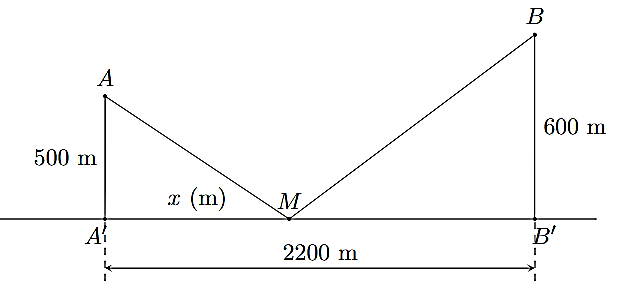
Có hai xã A, B cùng ở bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA' = 500 m, BB' = 600 m và người ta đo được A'B' = 2 200 m. Các kĩ sư muốn xây một trạm cung cấp nước sạch đó là điểm M trên đoạn
MA' = x (m), 0 < x < 2 200 (minh họa ở hình bên).
Sử dụng dữ kiện bài toán dưới đây để trả lời Bài 7, 8.
Có hai xã A, B cùng ở bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA' = 500 m, BB' = 600 m và người ta đo được A'B' = 2 200 m. Các kĩ sư muốn xây một trạm cung cấp nước sạch đó là điểm M trên đoạn
MA' = x (m), 0 < x < 2 200 (minh họa ở hình bên).
Tổng khoảng cách MA + MB theo x là:
A. \[\sqrt {{{500}^2} + {x^2}} \] + \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
B. \[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
C. \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \] − \[\sqrt {{{500}^2} + {x^2}} \].
D. −\[\sqrt {{{500}^2} + {x^2}} \] − \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Xét ∆AA'M vuông tại A' có MA = \[\sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{{500}^2} + {x^2}} \] (m).
Xét ∆BB'M vuông tại B' có MB = \[\sqrt {B{{B'}^2} + B'{M^2}} = \sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \] (m).
Khi đó MA + MB = \[\sqrt {{{500}^2} + {x^2}} \] + \[\sqrt {{{600}^2} + {{\left( {2200 - x} \right)}^2}} \] (m).
Câu hỏi cùng đoạn
Câu 2:
Tổng khoảng cách MA + MB khi x = 1200 là (làm tròn kết quả đến hàng đơn vị của mét)
A. 2 466 m.
B. 2 664 m.
C. 2 400 m.
D. 2 600 m.
Giải bởi Vietjack
Đáp án đúng là: A
Với x = 1 200, ta có:
MA + MB = \[\sqrt {{{500}^2} + {{1200}^2}} \] + \[\sqrt {{{600}^2} + {{\left( {2200 - 1200} \right)}^2}} \] ≈ 2 466 (m).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 4,5 m.
B. 10,9 m.
C. 19 m.
D. 9 m.
Lời giải
Đáp án đúng là: B
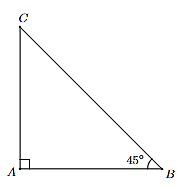
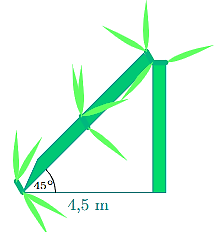
Xem đoạn bị gãy là CB, đoạn còn lại (thẳng đứng) là AC.
Như vậy, độ dài của cây khi chưa bị gãy là AC + BC.
Do tam giác ABC vuông tại A và \(\widehat {ABC}\) = 45°, suy ra tam giác ABC vuông cân tại A.
Suy ra AC = AB = 4,5 m.
Áp dụng định lí Pythagore trong tam giác ABC, ta có:
AB2 + AC2 = BC2
4,52 + 4,52 = BC2
Suy ra BC = \(\sqrt {2.4,{5^2}} = \sqrt {40,5} \) m.
Vậy chiều cao cây trước khi gãy là: 4,5 + \(\sqrt {40,5} \) ≈ 10,9 m.
Câu 2
A. 23,03 m.
B. 23,3 m.
C. 230,3 m.
D. 203 m.
Lời giải
Đáp án đúng là: C
Gọi cạnh hình vuông (nền kim tự tháp) là x, điều kiện x > 0, đơn vị m.
Diện tích hình vuông là: x2 = 53 052.
Suy ra x = \(\sqrt {53052} \) ≈ 230,3 m.
Vậy độ dài cạnh nền của kim tự tháp khoảng 230,3 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 1 404 m.
B. 1 044 m.
C. 1 400 m.
D. 1 440 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập