Khi bay vào không gian, trọng lượng P (N) của một phi hành gia ở vị trí cách mặt đất một độ cao h (m) được tính theo công thức P = \(\frac{{{{28014.10}^{12}}}}{{{{\left( {{{64.10}^5} + h} \right)}^2}}}\). Ở độ cao bao nhiêu mét thì trọng lượng của phi hành gia là 619 N? (làm tròn đến kết quả phần mười).
A. 327 322,3 (m).
B. 327 (m).
C. 327,3 (m).
D. 3 273,3 (m).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Vì trọng lượng của phi hành gia là 619 N nên ta có:
619 = \(\frac{{{{28014.10}^{12}}}}{{{{\left( {{{64.10}^5} + h} \right)}^2}}}\)
(64.105 + h)2 = \(\frac{{{{28014.10}^{12}}}}{{619}}\)
64.105 + h = \(\sqrt {\frac{{{{28014.10}^{12}}}}{{619}}} \)
h = \(\sqrt {\frac{{{{28014.10}^{12}}}}{{619}}} \) − 64.105 ≈ 327 322,3 (m).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Đổi 800 (km/h) = \(\frac{{2000}}{9}\) (m/s).
Khi đó, ta có:
\(\frac{{2000}}{9} = \sqrt {9,81d} \)
Suy ra 9,81d = \({\left( {\frac{{2000}}{9}} \right)^2}\)
Do đó, d = \({\left( {\frac{{2000}}{9}} \right)^2}\): 9,81 ≈ 5,034 m.
Câu 2
A. \(\sqrt 2 \) cm.
B. \(3\sqrt 2 \) cm.
C. \(2\sqrt 2 \) cm.
D. \(5\sqrt 2 \) cm.
Lời giải
Đáp án đúng là: C
Vì AMIN là hình vuông nên AM = IN = 2 cm và \(\widehat {ANI}\) = 90°.
Xét tam giác ANI vuông tại N, áp dụng định lý Pythagore, ta có:
AI2 = AN2 + IN2
Suy ra AI2 = 8, do đó AI = \(2\sqrt 2 \) (cm).
Câu 3
A. \(\sqrt 6 + \sqrt 3 \).
B. \(6\sqrt 6 \).
C. \(12 + 6\sqrt 2 \).
D. \(12 - 6\sqrt 2 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(40\sqrt 2 \) m.
B. \(30\sqrt 2 \) m.
C. \(50\sqrt 2 \) m.
D. \(120\sqrt 2 \) m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Một vườn hoa gồm ba hình vuông X, Y, Z lần lượt có diện tích như hình vẽ.
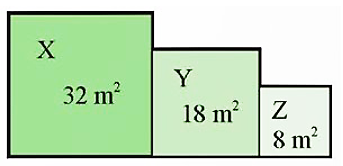
Chu vi của vườn hoa đó là:
A. \(12\sqrt 2 \) m.
B. \(8\sqrt 2 \) m.
C. \(16\sqrt 2 \) m.
D. \(36\sqrt 2 \) m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo