Câu hỏi:

09/01/2025 93

Biết rằng hình thang và hình chữ nhật có diện tích bằng nhau. Tính chiều cao h của hình thang.

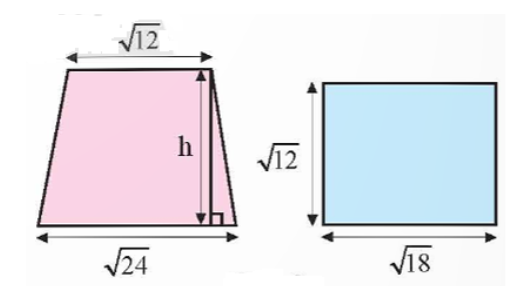
A. \(\sqrt 6 + \sqrt 3 \).

B. \(6\sqrt 6 \).

C. \(12 + 6\sqrt 2 \).

D. \(12 - 6\sqrt 2 \).

Xem lời giải

Câu hỏi trong đề: 12 bài tập Một số bài toán thực tế liên quan đến biểu thức có chứa căn thức bậc hai có lời giải !!

Bắt đầu thi

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: D

Diện tích hình chữ nhật là:

\(\sqrt {12} .\sqrt 8 = \sqrt {12.8} = 6\sqrt 6 \) (đvdt).

Vì hình thang và hình chữ nhật có diện tích bằng nhau nên diện tích hình thang là \(6\sqrt 6 \) (đvdt).

Khi đó, diện tích hình thang là: \(\frac{{\sqrt {24} + \sqrt {12} }}{2}.h = 6\sqrt 6 \).

Ta có: \(\frac{{\sqrt {24} + \sqrt {12} }}{2} = \frac{{\sqrt {4.6} + \sqrt {4.3} }}{2} = \frac{{2\sqrt 6 + 2\sqrt 3 }}{2} = \sqrt 6 + \sqrt 3 \).

Do đó, \(\left( {\sqrt 6 + \sqrt 3 } \right)h = 6\sqrt 6 \)

Suy ra h = \(\frac{{6\sqrt 6 }}{{\sqrt 6 + \sqrt 3 }} = \frac{{6\sqrt 6 \left( {\sqrt 6 - \sqrt 3 } \right)}}{{\left( {\sqrt 6 + \sqrt 3 } \right)\left( {\sqrt 6 - \sqrt 3 } \right)}} = \frac{{6\sqrt 6 \left( {\sqrt 6 - \sqrt 3 } \right)}}{3} = 2\sqrt 6 \left( {\sqrt 6 - \sqrt 3 } \right)\).

Vậy chiều cao của hình thang là h = \(2\sqrt 6 \left( {\sqrt 6 - \sqrt 3 } \right) = 12 - 6\sqrt 2 \).

Bình luận

Câu 1:

Ngày 28/9/2018, sau trận động đất 7,5 độ Richter, cơn sóng thần cao hơn 6 m đã tràn vào đảo Sulawesi (Indonesia) và tàn phá thành phpps Palu gây thiệt hại vô vùng to lớn. Tốc dộ cơn sóng thần v (m/s) và chiều sâu đại dương d (m) của nơi bắt đầu sóng thần liên hệ bởi công thức v = \(\sqrt {dg} \) trong đó g = 9,81 m/s².
Theo tính toán của các nhà khoa học địa chất, tốc độ cơn sóng thần ngày 28/9/2018 là 800 km/h. Hãy tính chiều sâu đại dương của nơi tâm chấn động đất gây ra sóng thần (làm tròn đến kết quả hàng đơn vị của mét).

A. 503,4 m.

B. 5,034 m.

C. 50,34 m.

D. 0,53 m.

Xem đáp án » 09/01/2025 380

Câu 2:

Khi bay vào không gian, trọng lượng P (N) của một phi hành gia ở vị trí cách mặt đất một độ cao h (m) được tính theo công thức P = \(\frac{{{{28014.10}^{12}}}}{{{{\left( {{{64.10}^5} + h} \right)}^2}}}\). Ở độ cao bao nhiêu mét thì trọng lượng của phi hành gia là 619 N? (làm tròn đến kết quả phần mười).

A. 327 322,3 (m).

B. 327 (m).

C. 327,3 (m).

D. 3 273,3 (m).

Xem đáp án » 09/01/2025 205

Câu 3:

Độ dài đường chéo của hình vuông AMIN là

A. \(\sqrt 2 \) cm.

B. \(3\sqrt 2 \) cm.

C. \(2\sqrt 2 \) cm.

D. \(5\sqrt 2 \) cm.

Xem đáp án » 09/01/2025 139

Câu 4:

Cạnh của thửa ruộng hình vuông lớn là:

A. \(40\sqrt 2 \) m.

B. \(30\sqrt 2 \) m.

C. \(50\sqrt 2 \) m.

D. \(120\sqrt 2 \) m.

Xem đáp án » 09/01/2025 125

Câu 5:

Trong thuyết tương đối, khối lượng m (kg) của một vật khi di chuyển với vận tốc v (m/s) được cho bởi công thức m = \(\frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), trong đó m₀ (kg) là khối lượng của vật khi đứng yên, c (m/s) là vận tốc của ánh sáng trong chân không.

a) Viết lại công thức tính khối lượng m dưới dạng không có căn thức ở mẫu.

b) Tính khối lượng m theo m₀ (làm tròn đến chữ số thập phân thứ ba) khi vật chuyển động với vận tốc v = \(\frac{1}{{10}}\)c.

Xem đáp án » 09/01/2025 90

Câu 6:

Một vườn hoa gồm ba hình vuông X, Y, Z lần lượt có diện tích như hình vẽ.

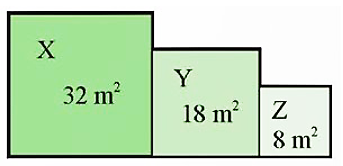
Chu vi của vườn hoa đó là:

A. \(12\sqrt 2 \) m.

B. \(8\sqrt 2 \) m.

C. \(16\sqrt 2 \) m.

D. \(36\sqrt 2 \) m.

Xem đáp án » 09/01/2025 80

Biết rằng hình thang và hình chữ nhật có diện tích bằng nhau. Tính chiều cao h của hình thang.

Cấp tốc 789+ thi vào lớp 10 môn Toán

Cấp tốc 789+ thi vào lớp 10 môn Ngữ Văn

Cấp tốc 789+ thi vào lớp 10 môn Tiếng Anh