Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {1;0;2} \right)\) và vuông góc với đường thẳng \(d:\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 2}}{3}\) có phương trình là
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {1;0;2} \right)\) và vuông góc với đường thẳng \(d:\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 2}}{3}\) có phương trình là
A. \(2x + y - 3z - 8 = 0\).
B. \(2x - y + 3z - 8 = 0\).
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Ta có \(\overrightarrow {{u_d}} = \left( {2; - 1;3} \right)\).
Vì \(d \bot \left( P \right)\) nên mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2; - 1;3} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {1;0;2} \right)\) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2; - 1;3} \right)\) có phương trình là \(2\left( {x - 1} \right) - y + 3\left( {z - 2} \right) = 0\)\( \Leftrightarrow 2x - y + 3z - 8 = 0\). Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét các biến cố:
\({A_1}\): Sản phẩm lấy ra lần thứ nhất bị lỗi. Khi đó, ta có: \(P\left( {{A_1}} \right) = \frac{{39}}{{2000}}\); \(P\left( {\overline {{A_1}} } \right) = \frac{{1961}}{{2000}}\).
\({A_2}\): Sản phẩm lấy ra lần thứ hai bị lỗi.
Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn \(1999\) sản phẩm và trong đó có \(38\) sản phẩm lỗi nên ta có: \(P\left( {{A_2}\left| {{A_1}} \right.} \right) = \frac{{38}}{{1999}}\), suy ra \(P\left( {\overline {{A_2}} \left| {{A_1}} \right.} \right) = \frac{{1961}}{{1999}}\).
Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn \(1999\) sản phẩm trong đó có \(39\)sản phẩm lỗi nên ta có: \(P\left( {{A_2}\left| {\overline {{A_1}} } \right.} \right) = \frac{{39}}{{1999}}\), suy ra \(P\left( {\overline {{A_2}} \left| {\overline {{A_1}} } \right.} \right) = \frac{{1960}}{{1999}}\).
Khi đó, xác suất để sản phẩm lấy ra lần thứ hai bị lỗi là:
\(P\left( {{A_2}} \right) = P\left( {{A_2}\left| {{A_1}} \right.} \right) \cdot P\left( {{A_1}} \right) + P\left( {{A_2}\left| {\overline {{A_1}} } \right.} \right) \cdot P\left( {\overline {{A_1}} } \right)\)\( = \frac{{38}}{{1999}} \cdot \frac{{39}}{{2000}} + \frac{{39}}{{1999}} \cdot \frac{{1961}}{{2000}} \approx 0,02\).
Đáp án: \(0,02\)
Lời giải
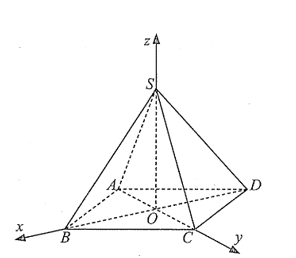
Ta có \(AB = 2\sqrt 2 \)\( \Rightarrow OA = OB = 2\)\( \Rightarrow A\left( {0; - 2;0} \right)\). Ta có \(OB = 2 \Rightarrow B\left( {2;0;0} \right)\).
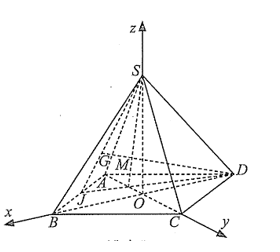
\(OS = \sqrt {S{A^2} - O{A^2}} = \sqrt {16 - 4} = 2\sqrt 3 \Rightarrow S\left( {0;0;2\sqrt 3 } \right)\).
Suy ra tọa độ của trọng tâm của tam giác \(SAB\) là\(G\left( {\frac{2}{3}; - \frac{2}{3};\frac{{2\sqrt 3 }}{3}} \right)\).
Ta có \(C\left( {0;2;0} \right)\)\( \Rightarrow \overrightarrow {CE} = \left( {a; - 2;b} \right)\), \(\overrightarrow {CG} = \left( {\frac{2}{3}; - \frac{8}{3};\frac{{2\sqrt 3 }}{3}} \right)\).
Vì \(C,E,G\) thẳng hàng nên \(\overrightarrow {CE} \) cùng phương với \(\overrightarrow {CG} \)
\( \Rightarrow \frac{{3a}}{2} = \frac{3}{4} = \frac{{b\sqrt 3 }}{2}\)\( \Rightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = \frac{{\sqrt 3 }}{2}\end{array} \right.\)\( \Rightarrow a \cdot b = \frac{{\sqrt 3 }}{4}\).
Do \(D\) đối xứng với \(B\) qua mặt phẳng \(\left( {Oyz} \right)\) nên với mọi điểm \(M\) trên mặt phẳng \(\left( {Oyz} \right)\), ta đều có \(MG + MB = MG + MD\).
Mặt khác, hai điểm \(G\) và \(D\) khác phía so với mặt phẳng \(\left( {Oyz} \right)\) nên \(MG + MD\) nhỏ nhất khi và chỉ khi ba điểm \(G,D,M\) thẳng hàng.
Ta có \(D\left( { - 2;0;0} \right)\), \(\overrightarrow {DM} = \left( {2;m;n} \right),\overrightarrow {DG} = \left( {\frac{8}{3}; - \frac{2}{3};\frac{{2\sqrt 3 }}{3}} \right)\).
Vì \(G,D,M\) thẳng hàng nên \(\overrightarrow {DM} \) cùng phương với \(\overrightarrow {DG} \)
\( \Rightarrow \frac{3}{4} = - \frac{{3m}}{2} = \frac{{n\sqrt 3 }}{2}\)\( \Rightarrow \left\{ \begin{array}{l}m = - \frac{1}{2}\\n = \frac{{\sqrt 3 }}{2}\end{array} \right.\)\( \Rightarrow {m^2} + {n^2} = 1\).
Đáp án: a) Sai, b) Đúng, c) Sai, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.