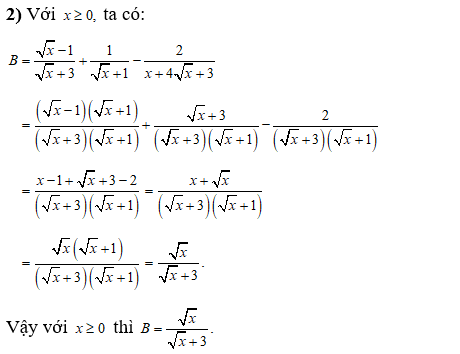Câu hỏi:
11/03/2025 422Quảng cáo
Trả lời:
Giải bởi Vietjack
Thay (thỏa mãn) vào biểu thức A có:
Vậy khi thì
Câu hỏi cùng đoạn
Câu 3:
3) Tìm giá trị của x để biểu thức đạt giá trị lớn nhất.
3) Tìm giá trị của x để biểu thức đạt giá trị lớn nhất.
Lời giải của GV VietJack
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi \(a,\,\,b\) lần lượt là số thanh có độ dài là \(0,7\,{\rm{m}}\) và \(0,5\,{\rm{m}}\) được cắt nhỏ từ thanh sắt dài \(7,4\,{\rm{m}}\) \(\left( {a \in \mathbb{N},\,\,b \in \mathbb{N}} \right).\)
Khi đó, ta có phương trình \(0,7a + 0,5b = 7,4\) hay \(7a + 5b = 74.\)
Suy ra \(b = \frac{{74 - 7a}}{5} = 15 - a - \frac{{1 + 2a}}{5}.\)
Vì \(b \in \mathbb{N}\) nên \(\left( {1 + 2a} \right)\,\, \vdots \,\,5\) hay \(\left( {1 + 2a} \right) \in \left\{ {0;\,\,5;\,\,10;\,\,15;\,\,20;\,\,25;\,\,...} \right\}\)
Mà \(1 + 2a\) là số lẻ nên \(\left( {1 + 2a} \right) \in \left\{ {5;\,\,15;\,\,25;\,\,...} \right\}\) suy ra \(a \in \left\{ {2;\,\,7;\,\,12;\,\,...} \right\}\)
Lại có \(74 = 7a + 5b \ge 7a\) nên \(a \le \frac{{74}}{7}.\) Suy ra \(0 \le a \le 10\) nên \(a \in \left\{ {2;\,\,7} \right\}.\)
Với \[a = 2,\] ta có \[b = 12\] (thỏa mãn).
Với \(a = 7,\) ta có \(b = 5\) (thỏa mãn).
Như vậy, có 2 cách cắt mỗi thanh sắt dài \(7,4\,{\rm{m}}\) thành các thanh có độ dài là \(0,7\,{\rm{m}}\) và \(0,5\,{\rm{m}}{\rm{.}}\)
Cách 1: Cắt thanh sắt dài \(7,4\,{\rm{m}}\) thành 2 thanh \(0,7\,{\rm{m}}\) và 12 thanh \(0,5\,{\rm{m}}{\rm{.}}\)
Cách 2: Cắt thanh sắt dài \(7,4\,{\rm{m}}\) thành 7 thanh dài \(0,7\,{\rm{m}}\) và 5 thanh dài \(0,5\,{\rm{m}}{\rm{.}}\)
⦁ Theo đề bài cần cắt \(1000\) đoạn dài \(0,7\,{\rm{m}}\) và \(2000\) đoạn dài \(0,5\,{\rm{m}}{\rm{.}}\)
Do đó, nếu cắt theo cách 1 cần \(500\) cây sắt dài \(7,4\,{\rm{m}}\) khi đó thừa \(\left( {500:2} \right) \cdot 12 - 2000 = 1000\) đoạn \(0,5\,{\rm{m}}\) lãng phí.
Nếu cắt theo cách 2 thì cần \(400\) cây sắt dài \(7,4\,{\rm{m}}\) khi đó thừa \(\left( {2000:5} \right) \cdot 7 - 1000 = 1800\) đoạn dài \(0,7\,{\rm{m}}\) lãng phí.
Do vậy để tiết kiệm ta sẽ dùng cả 2 cách cắt trên.
⦁ Gọi \(x\) là số cây sắt dài \(7,4\,{\rm{m}}\) dùng để cắt theo cách 1, \(y\) là số cây sắt dài \(7,4\,{\rm{m}}\) dùng để cắt theo cách 2 \((x,\,y\) là các số tự nhiên khác 0)
Số đoạn sắt dài \(0,7\,{\rm{m}}\) là: \(2x + 7y\) đoạn.
Số đoạn sắt dài \(0,5\,{\rm{m}}\) là \(12x + 5y\) đoạn.
Vì cần \(1000\) đoạn dài \(0,7\,{\rm{m}}\) và \(2000\) đoạn \(0,5\,{\rm{m}}\) nên ta có hệ phương trình: \[\left\{ \begin{array}{l}2x + 7y = 1000\\12x + 5y = 2000\end{array} \right.\]
Giải hệ phương trình trên, ta được \(x \approx 121,6\) và \(y \approx 108,1.\)
Ta lấy \(x = 121\) và \(y = 108\) thì sẽ cắt được tổng là \(2 \cdot 121 + 7 \cdot 108 = 998\) đoạn \(0,7\,{\rm{m}}\) và \[12 \cdot 121 + 5 \cdot 108 = 1992\] đoạn \(0,5\,{\rm{m}}.\)
Ta chỉ cần cắt thêm 1 thanh theo cách 1 (thêm 2 thanh \(0,7\,{\rm{m}}\) và 12 thanh \(0,5\,{\rm{m),}}\) tức là đã dùng \(121 + 108 + 1 = 230\) thanh sắt \(7,4\,{\rm{m}}.\)
Điều quan trọng lúc này chúng ta cần chỉ ra rằng cách này là tiết kiệm nhất.
Thật vậy, ta thấy tổng số độ dài của \(1000\) đoạn \(0,7{\rm{\;m}}\) và \(2000\) đoạn \(0,5\,{\rm{m}}\) là:
\(1000 \cdot 0,7 + 2000 \cdot 0,5 = 1\,\,700{\rm{\;(m)}}{\rm{.}}\)
Như vậy, phải dùng ít nhất là \(1700:7,4 \approx 229,7 \approx 230\) thanh sắt \(7,4\,{\rm{m}}.\)
Vậy cần cắt 122 thanh theo cách 1 và 108 thanh theo cách 2 thì thỏa mãn yêu cầu đề bài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Tháng 1) năm học 2025 - 2026_Môn Toán_THCS Cầu Giấy_Quận Cầu Giấy
Nhắn tin Zalo