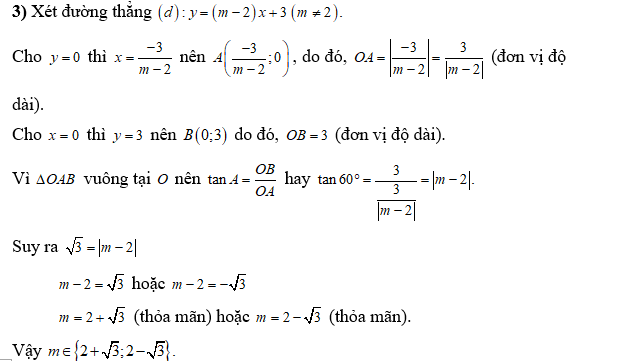Câu hỏi:
11/03/2025 516
(4,0 điểm)
2) Cho đường tròn (O) đường kính AB=2R. Lấy điểm C trên đường tròn (O) và lấy điểm M bất kì trên cung nhỏ BC (M không trùng với B,C). Gọi H là giao điểm của AM và BC. Đường thẳng AC cắt đường thẳng BM tại D. DH cắt AB tại K.
a) Chứng minh rằng bốn điểm cùng thuộc một đường tròn.
(4,0 điểm)
2) Cho đường tròn (O) đường kính AB=2R. Lấy điểm C trên đường tròn (O) và lấy điểm M bất kì trên cung nhỏ BC (M không trùng với B,C). Gọi H là giao điểm của AM và BC. Đường thẳng AC cắt đường thẳng BM tại D. DH cắt AB tại K.
a) Chứng minh rằng bốn điểm cùng thuộc một đường tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét đường tròn (O;R) có là góc nội tiếp chắn nửa đường tròn nên hay suy ra hay tam giác DCH vuông tại C suy ra ba điểm D,C,H cùng thuộc đường tròn ngoại tiếp tam giác DCH có tâm là trung điểm của DH và bán kính bằng (đường tròn đường kính DH)
Chứng minh tương tự ta có ba điểm D,M,H cùng thuộc đường tròn đường kính DH.Vậy bốn điểm C,D,M,H cùng thuộc đường tròn đường kính DH
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng đồng dạng với .
b) Chứng minh rằng đồng dạng với .
Lời giải của GV VietJack
b) Ta có bốn điểm A,B,M,C cùng nằm trên đường tròn (O;R) nên tứ giác ABMC nội tiếp đường tròn, suy ra (tổng hai góc đối của tứ giác nội tiếp).
Mà (kề bù) nên hay
là các góc nội tiếp chắn cung CM suy ra hay
Xét và có: là góc chung và (chứng minh trên)
Do đó (g.g).
Câu 3:
c) Chứng minh rằng .
c) Chứng minh rằng .
Lời giải của GV VietJack
c) Xét đường tròn (O;R) có lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung CM nên (1)
Chứng minh tương tự câu a ta có bốn điểm cùng thuộc một đường tròn hay tứ giác ACHK nội tiếp đường tròn, nên (hai góc nội tiếp cùng chắn cung CH) hay
Chứng minh tương tự, ta có .
Lại có (hai góc nội tiếp cùng chắn cung CM của đường tròn (O)) nên hay KH là tia phân giác của suy ra (2)
Từ (1) và (2) suy ra
Câu 4:
d) Kẻ phân giác góc \(AMB\) cắt \(AB\) tại \(P\). Tìm vị trí của \(M\) thỏa mãn đề bài để \(\frac{{MP}}{{MA + MB}}\) đạt giá trị lớn nhất.
Lời giải của GV VietJack
d) Ta có MP là tia phân giác của nên
Gọi Q là giao điểm của MP với đường tròn (O;R) Khi đó (góc nội tiếp chắn nửa đường tròn) và (hai góc nội tiếp cùng chắn cung AQ của đường tròn (O))
Suy ra vuông cân tại Q
Do đó hay nênXét và có: (chứng minh trên) và (đối đỉnh)
Do đó (g.g). Suy ra hay
Tương tự (g.g), suy ra
Do đó (do vì vuông cân tại Q.)
¬ Chứng minh bất đẳng thức bổ đề: Với \(x > 0,\,\,y > 0\) ta luôn có \(\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}.\)
Thật vậy, với \(x > 0,\,\,y > 0\) ta có: \({\left( {x - y} \right)^2} \ge 0\)
\({x^2} - 2xy + {y^2} \ge 0\)
\({x^2} + 2xy + {y^2} \ge 4xy\)
\(\frac{{{{\left( {x + y} \right)}^2}}}{{xy\left( {x + y} \right)}} \ge \frac{{4xy}}{{xy\left( {x + y} \right)}}\)
\(\frac{{x + y}}{{xy}} \ge \frac{4}{{x + y}}\)
\[\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\].
Dấu “=” xảy ra khi và chỉ khi \({\left( {x - y} \right)^2} = 0\) hay \(x = y.\) Bất đẳng thức trên đã được chứng minh.
Áp dụng bất đẳng thức trên, ta có: \(\frac{1}{{MA}} + \frac{1}{{MB}} \ge \frac{4}{{MA + MB}}\)
Hay \(\frac{{MP}}{{MA + MB}} \le MP \cdot \frac{1}{4}\left( {\frac{1}{{MA}} + \frac{1}{{MB}}} \right) = \frac{1}{4} \cdot \left( {\frac{{MP}}{{MA}} + \frac{{MP}}{{MB}}} \right) = \frac{{\sqrt 2 }}{4}.\)
Dấu “=” xảy ra khi và chỉ khi \(MA = MB.\)
Vậy giá trị lớn nhất của \(\frac{{MP}}{{MA + MB}}\) là \(\frac{{\sqrt 2 }}{4}\) khi \(MA\, = \,MB\) hay \(M\) là điểm chính giữa cung \(AB.\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi \(a,\,\,b\) lần lượt là số thanh có độ dài là \(0,7\,{\rm{m}}\) và \(0,5\,{\rm{m}}\) được cắt nhỏ từ thanh sắt dài \(7,4\,{\rm{m}}\) \(\left( {a \in \mathbb{N},\,\,b \in \mathbb{N}} \right).\)
Khi đó, ta có phương trình \(0,7a + 0,5b = 7,4\) hay \(7a + 5b = 74.\)
Suy ra \(b = \frac{{74 - 7a}}{5} = 15 - a - \frac{{1 + 2a}}{5}.\)
Vì \(b \in \mathbb{N}\) nên \(\left( {1 + 2a} \right)\,\, \vdots \,\,5\) hay \(\left( {1 + 2a} \right) \in \left\{ {0;\,\,5;\,\,10;\,\,15;\,\,20;\,\,25;\,\,...} \right\}\)
Mà \(1 + 2a\) là số lẻ nên \(\left( {1 + 2a} \right) \in \left\{ {5;\,\,15;\,\,25;\,\,...} \right\}\) suy ra \(a \in \left\{ {2;\,\,7;\,\,12;\,\,...} \right\}\)
Lại có \(74 = 7a + 5b \ge 7a\) nên \(a \le \frac{{74}}{7}.\) Suy ra \(0 \le a \le 10\) nên \(a \in \left\{ {2;\,\,7} \right\}.\)
Với \[a = 2,\] ta có \[b = 12\] (thỏa mãn).
Với \(a = 7,\) ta có \(b = 5\) (thỏa mãn).
Như vậy, có 2 cách cắt mỗi thanh sắt dài \(7,4\,{\rm{m}}\) thành các thanh có độ dài là \(0,7\,{\rm{m}}\) và \(0,5\,{\rm{m}}{\rm{.}}\)
Cách 1: Cắt thanh sắt dài \(7,4\,{\rm{m}}\) thành 2 thanh \(0,7\,{\rm{m}}\) và 12 thanh \(0,5\,{\rm{m}}{\rm{.}}\)
Cách 2: Cắt thanh sắt dài \(7,4\,{\rm{m}}\) thành 7 thanh dài \(0,7\,{\rm{m}}\) và 5 thanh dài \(0,5\,{\rm{m}}{\rm{.}}\)
⦁ Theo đề bài cần cắt \(1000\) đoạn dài \(0,7\,{\rm{m}}\) và \(2000\) đoạn dài \(0,5\,{\rm{m}}{\rm{.}}\)
Do đó, nếu cắt theo cách 1 cần \(500\) cây sắt dài \(7,4\,{\rm{m}}\) khi đó thừa \(\left( {500:2} \right) \cdot 12 - 2000 = 1000\) đoạn \(0,5\,{\rm{m}}\) lãng phí.
Nếu cắt theo cách 2 thì cần \(400\) cây sắt dài \(7,4\,{\rm{m}}\) khi đó thừa \(\left( {2000:5} \right) \cdot 7 - 1000 = 1800\) đoạn dài \(0,7\,{\rm{m}}\) lãng phí.
Do vậy để tiết kiệm ta sẽ dùng cả 2 cách cắt trên.
⦁ Gọi \(x\) là số cây sắt dài \(7,4\,{\rm{m}}\) dùng để cắt theo cách 1, \(y\) là số cây sắt dài \(7,4\,{\rm{m}}\) dùng để cắt theo cách 2 \((x,\,y\) là các số tự nhiên khác 0)
Số đoạn sắt dài \(0,7\,{\rm{m}}\) là: \(2x + 7y\) đoạn.
Số đoạn sắt dài \(0,5\,{\rm{m}}\) là \(12x + 5y\) đoạn.
Vì cần \(1000\) đoạn dài \(0,7\,{\rm{m}}\) và \(2000\) đoạn \(0,5\,{\rm{m}}\) nên ta có hệ phương trình: \[\left\{ \begin{array}{l}2x + 7y = 1000\\12x + 5y = 2000\end{array} \right.\]
Giải hệ phương trình trên, ta được \(x \approx 121,6\) và \(y \approx 108,1.\)
Ta lấy \(x = 121\) và \(y = 108\) thì sẽ cắt được tổng là \(2 \cdot 121 + 7 \cdot 108 = 998\) đoạn \(0,7\,{\rm{m}}\) và \[12 \cdot 121 + 5 \cdot 108 = 1992\] đoạn \(0,5\,{\rm{m}}.\)
Ta chỉ cần cắt thêm 1 thanh theo cách 1 (thêm 2 thanh \(0,7\,{\rm{m}}\) và 12 thanh \(0,5\,{\rm{m),}}\) tức là đã dùng \(121 + 108 + 1 = 230\) thanh sắt \(7,4\,{\rm{m}}.\)
Điều quan trọng lúc này chúng ta cần chỉ ra rằng cách này là tiết kiệm nhất.
Thật vậy, ta thấy tổng số độ dài của \(1000\) đoạn \(0,7{\rm{\;m}}\) và \(2000\) đoạn \(0,5\,{\rm{m}}\) là:
\(1000 \cdot 0,7 + 2000 \cdot 0,5 = 1\,\,700{\rm{\;(m)}}{\rm{.}}\)
Như vậy, phải dùng ít nhất là \(1700:7,4 \approx 229,7 \approx 230\) thanh sắt \(7,4\,{\rm{m}}.\)
Vậy cần cắt 122 thanh theo cách 1 và 108 thanh theo cách 2 thì thỏa mãn yêu cầu đề bài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Tháng 1) năm học 2025 - 2026_Môn Toán_THCS Cầu Giấy_Quận Cầu Giấy
Nhắn tin Zalo