Câu hỏi:
11/03/2025 176
Câu 6-7: (2,0 điểm)
1) Nhân dịp đầu học kỳ 2, Liên đội trường THCS phát động phong trào ủng hộ đồ dùng học tập cho các bạn khó khăn trong trường. Hưởng ứng tinh thần tương thân tương ái, hai bạn An và Bảo vào siêu thị mua vở và bút bi để ủng hộ các bạn. Bạn An mua 5 quyển vở và 3 chiếc bút bi với tổng số tiền phải trả 39 000 đồng. Bạn Bảo mua 6 quyển vở và 2 chiếc bút bi với tổng số tiền phải trả là 42 000 đồng. Hỏi giá mỗi quyển vở và mỗi chiếc bút bi bao nhiêu tiền?
Câu 6-7: (2,0 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi giá tiền mua một quyển vở là \(x\) (đồng), giá tiền mua một chiếc bút bi là \[y\] (đồng) \(\left( {x > 0,\,\,y > 0} \right).\)
Bạn An mua 5 quyển vở và 3 chiếc bút bi với tổng số tiền phải trả 39 000 đồng nên ta có phương trình \(5x + 3y = 39\,\,000\) (1)
Bạn Bảo mua 6 quyển vở và 2 chiếc bút bi với tổng số tiền phải trả là 42 000 đồng, ta có phương trình \(6x + 2y = 42\,\,000\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x + 3y = 39\,\,000}\\{6x + 2y = 42\,\,000}\end{array}} \right.\)
Giải hệ phương trình trên, ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 6\,\,000}\\{y = 3\,\,000}\end{array}} \right.\) (thỏa mãn).
Vậy giá mỗi quyển vở là 6 000 đồng, giá mỗi cái bút bi là 3 000 đồng.
Câu hỏi cùng đoạn
Câu 2:
2) Hải đăng Kê Gà cao 65 m ở mũi Kê Gà thuộc tỉnh Bình Thuận đã được trung tâm sách kỷ lục Việt Nam xác nhận là ngọn hải đăng cao nhất và cổ xưa nhất Việt Nam. Một người đang ở trên đài quan sát của ngọn hải đăng này nhìn thấy một chiếc tàu ở xa với góc \(30^\circ \)(như hình vẽ). Hỏi khoảng cách từ tàu đến chân hải đăng là bao nhiêu (làm tròn đến mét)?
Lời giải của GV VietJack
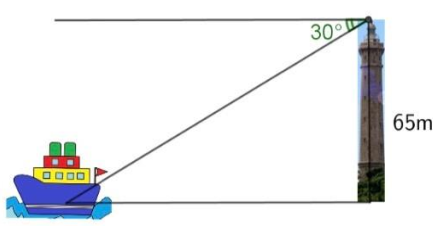
Gọi chiều cao của hải đăng là \(h,\) khoảng cách từ tàu đến chân hải đăng là \(a.\)
Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(h = a \cdot \tan \alpha \) suy ra \(a = \frac{h}{{\tan 30^\circ }} = \frac{{65}}{{\tan 30^\circ }} = 65\sqrt 3 \approx 113{\rm{\;(m)}}{\rm{.}}\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giải bất phương trình:
\(\left( {x - 1} \right)\left( {2x + 3} \right) < 2{x^2} - 4\left( {2 - x} \right)\)
\(2{x^2} + 3x - 2x - 3 < 2{x^2} - 8 + 4x\)
\(2{x^2} + 3x - 2x - 2{x^2} - 4x < - 8 + 3\)
\( - 3x < - 5\)
\(x > \frac{5}{3}.\)
Vậy nghiệm của bất phương trình là \(x > \frac{5}{3}.\)
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước