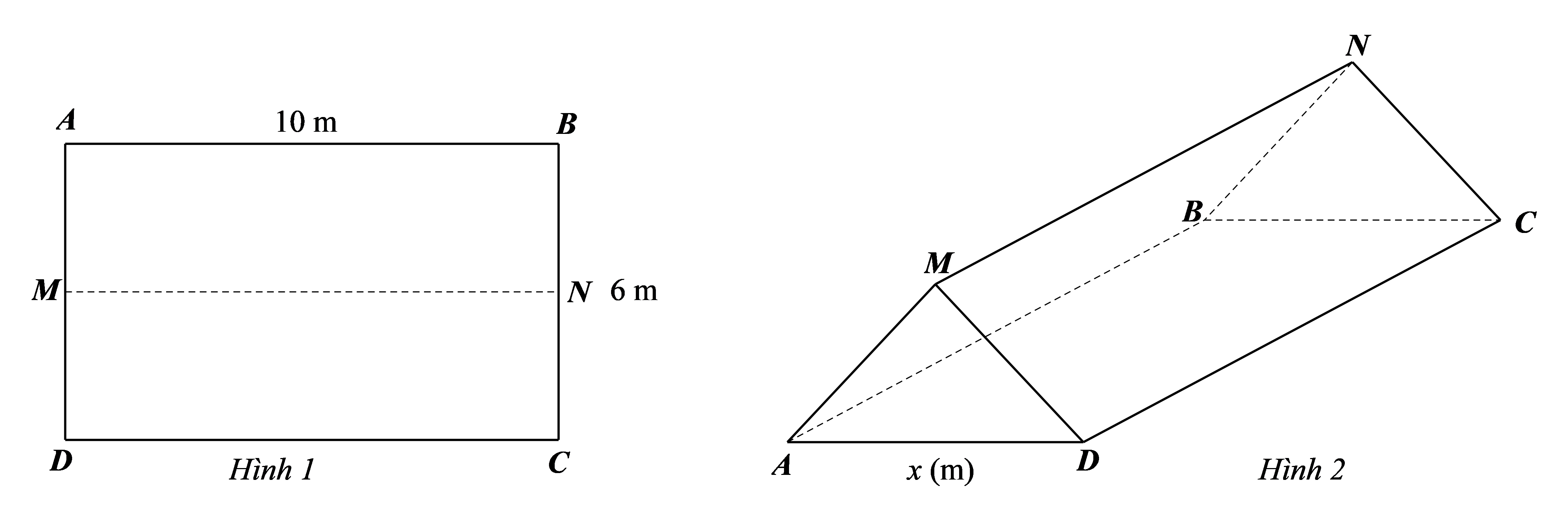Câu hỏi:
11/03/2025 438
Câu 6-8 (2,5 điểm)
1) Bác Tiến chia số tiền 400 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi thu được là 27 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là \(6\% /\)năm và khoản đầu tư thứ hai là \(8\% /\)năm. Tính số tiền bác Tiến đầu tư cho mỗi khoản.
Câu 6-8 (2,5 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cách 1: Giải bài toán bằng cách lập phương trình
Gọi số tiền ở khoản đầu tư thứ nhất của Bác Tiến là \(x\) (triệu đồng) \(\left( {0 \le x \le 400} \right).\)
Số tiền ở khoản đầu tư thứ hai là: \(400 - x\) (triệu đồng).
Số tiền lãi sau một năm ở khoản đầu tư thứ nhất là: \(6\% x = 0,06x\) (triệu đồng).
Số tiền lãi sau một năm ở khoản đầu tư thứ hai là: \(8\% \left( {400 - x} \right) = 32 - 0,08x\) (triệu đồng).
Theo bài, tổng số tiền lãi bác Tiến nhận được là 27 triệu đồng nên ta có phương trình:
\(0,06x + 32 - 0,08x = 27\).
Giải phương trình:
\(0,06x + 32 - 0,08x = 27\)
\( - 0,02x = 27 - 32\)
\( - 0,02x = - 5\)
\(x = 250\) (thoả mãn điều kiện).
Vậy số tiền ở khoản đầu tư thứ nhất là 250 triệu đồng và ở khoản đầu tư thứ hai là \(400 - 250 = 150\) (triệu đồng).
Cách 2: Giải bài toán bằng cách lập hệ phương trình
Gọi số tiền ở khoản đầu tư thứ nhất và thứ hai của Bác Tiến lần lượt là \(x\) và \(y\) (triệu đồng) \(\left( {0 \le x \le 400,\,\,0 \le y \le 400} \right).\)
Theo bài, tổng số tiền đầu tư của bác Tiến là 400 triệu đồng nên ta có phương trình:
\(x + y = 400\) (1)
Số tiền lãi sau một năm ở khoản đầu tư thứ nhất là: \(6\% x = 0,06x\) (triệu đồng).
Số tiền lãi sau một năm ở khoản đầu tư thứ hai là: \(8\% y = 0,08y\) (triệu đồng).
Theo bài, tổng số tiền lãi bác Tiến nhận được là 27 triệu đồng nên ta có phương trình:
\(0,06x + 0,08y = 27\) (2)
Từ phương trình (1) và (2) ta có hệ phương trình: \[\left\{ \begin{array}{l}x + y = 400\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\0,06x + 0,08y = 27\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Từ phương trình (1) ta có: \(y = 400 - x\) (3)
Thế vào phương trình (2) ta được: \(0,06x + 0,08\left( {400 - x} \right) = 27.\) (4)
Giải phương trình (4):
\(0,06x + 0,08\left( {400 - x} \right) = 27\)
\(0,06x + 32 - 0,08x = 27\)
\( - 0,02x = 27 - 32\)
\( - 0,02x = - 5\)
\(x = 250\) (thoả mãn điều kiện).
Thay giá trị \(x = 250\) vào phương trình (3) ta được: \(y = 400 - 250 = 150\)(thoả mãn điều kiện).
Vậy số tiền ở khoản đầu tư thứ nhất là 250 triệu đồng và ở khoản đầu tư thứ hai là 150 triệu đồng.
Câu hỏi cùng đoạn
Câu 2:
2) Một tổ sản xuất có kế hoạch làm 300 sản phẩm cùng loại trong một số ngày quy định. Thực tế, mỗi ngày tổ đã làm được nhiều hơn 10 sản phẩm so với số sản phẩm dự định làm trong một ngày theo kế hoạch. Vì thế tổ đã hoàn thành công việc sớm hơn kế hoạch 1 ngày. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phẩm mà tổ đó làm được trong mỗi ngày là bằng nhau).
Lời giải của GV VietJack
Giả sử theo kế hoạch mỗi ngày tổ sản xuất phải làm \(x\) (sản phẩm) \(\left( {x \in \mathbb{N}*,{\mkern 1mu} {\mkern 1mu} x < 300} \right).\)
Khi đó, theo kế hoạch thời gian cần thiết để làm xong 300 sản phẩm là: \(\frac{{300}}{x}\) (ngày).
Thực tế mỗi ngày số sản phẩm mà tổ làm được là: \(x + 10\) (sản phẩm).
Khi đó, thời gian thực tế mà tổ sản xuất làm xong 300 sản phẩm là: \(\frac{{300}}{{x + 10}}\) (ngày).
Do tổ đã hoàn thành công việc sớm hơn 1 ngày nên ta có phương trình:
\(\frac{{300}}{x} - \frac{{300}}{{x + 10}} = 1\) (1)
Giải phương trình (1):
\(\frac{{300}}{x} - \frac{{300}}{{x + 10}} = 1\)
\(\frac{1}{x} - \frac{1}{{x + 10}} = \frac{1}{{300}}\)
\(\frac{{x + 10 - x}}{{x\left( {x + 10} \right)}} = \frac{1}{{300}}\)
\(\frac{{10}}{{{x^2} + 10x}} = \frac{1}{{300}}\)
\({x^2} + 10x = 3\,\,000\)
\({x^2} - 50x + 60x - 3\,\,000 = 0\)
\(x\left( {x - 50} \right) + 60\left( {x - 50} \right) = 0\)
\(\left( {x - 50} \right)\left( {x + 60} \right) = 0\)
\(x - 50 = 0\) hoặc \(x + 60 = 0\)
\(x = 50\) (thoả mãn) \(x = - 60\) (không thoả mãn).
Vậy theo kế hoạch mỗi ngày tổ sản xuất cần sản xuất 50 sản phẩm.
Câu 3:
Lời giải của GV VietJack
Để phương trình \({x^2} - 3x + a = 0\) nhận \(x = \frac{{3 - \sqrt 5 }}{2}\) làm một nghiệm thì \(x = \frac{{3 - \sqrt 5 }}{2}\) phải thỏa mãn phương trình đó.
Thay \(x = \frac{{3 - \sqrt 5 }}{2}\) vào phương trình \({x^2} - 3x + a = 0\), ta được:
\({\left( {\frac{{3 - \sqrt 5 }}{2}} \right)^2} - 3 \cdot \left( {\frac{{3 - \sqrt 5 }}{2}} \right) + a = 0\)
\(\frac{{9 - 6\sqrt 5 + 5}}{4} - \frac{{9 - 3\sqrt 5 }}{2} + a = 0\)
\(\frac{{9 - 6\sqrt 5 + 5 - 18 + 6\sqrt 5 }}{4} + a = 0\)
\(\frac{{ - 4}}{4} + a = 0\)
\( - 1 + a = 0\)
\(a = 1\).
Với \(a = 1\), phương trình bậc hai trở thành: \({x^2} - 3x + 1 = 0\) (1)
Do phương trình (1) có hai nghiệm nên theo hệ thức Viète ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = 1.\end{array} \right.\)
Ta có \(x_1^2 + x_2^2 = x_1^2 + 2{x_1}{x_2} + x_2^2 - 2{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {3^2} - 2 \cdot 1 = 7.\)
Vậy \(a = 1\) và tổng bình phương hai nghiệm của phương trình đã cho khi ấy bằng 7.
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
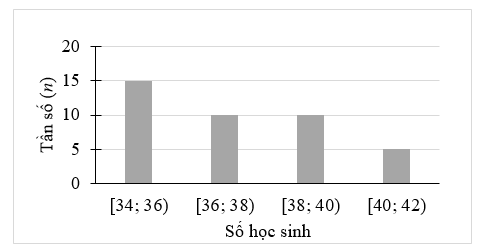
Tần số ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là 5.
Tần số tương đối ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là: \(f = \frac{5}{{40}} \cdot 100\% = 12,5\% .\)
Lời giải
a) Bán kính đáy của lý nước có dạng hình trụ đó là: \(\frac{5}{2} = 2,5{\rm{\;(cm)}}{\rm{.}}\)
Thể tích lượng nước tinh khiết được chứa trong ly bằng thể tích của hình trụ có chiều cao \(10\) cm, và bằng:
\({V_1} = \pi \cdot {\left( {2,5} \right)^2} \cdot 10 = 62,5\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa