Câu 11-13 ( 3 điểm) Cho đường tròn \(\left( O \right)\) có hai đường kính \(AB\) và \(MN\) vuông góc với nhau. Trên tia đối của tia \(MA\) lấy điểm \(C\) khác điểm \(M.\) Gọi \(H\) là chân đường vuông góc kẻ từ điểm \(M\) đến đường thẳng \(BC.\)
a) Chứng minh bốn điểm \(O,\,\,M,\,\,H,\,\,B\) cùng thuộc một đường tròn.
Quảng cáo
Trả lời:

a) Cách 1: Ta có \(MN \bot AB\) tại \[O\] nên \(\Delta MOB\) vuông tại \[O\], suy ra ba điểm \[M,{\rm{ }}O,{\rm{ }}B\] cùng thuộc đường tròn đường kính \[MB\].
Ta có \(MH \bot CB\) tại \[H\] nên \(\Delta MHB\) vuông tại \[H,\]suy ra ba điểm \[M,{\rm{ }}H,{\rm{ }}B\] cùng thuộc đường tròn đường kính \[MB\].
Do đó bốn điểm \[O;{\rm{ }}M;{\rm{ }}H;{\rm{ }}B\] cùng thuộc đường tròn đường kính \[MB\].
Cách 2: Gọi \[I\] là trung điểm của \[MB\].
Ta có \(MN \bot AB\) tại \[O\] nên \(\Delta MOB\) vuông tại \[O,\] lại có \[OI\] là đường trung tuyến ứng với cạnh huyền \(MB\) nên \(IO = IM = IB = \frac{1}{2}MB.\)Ta có \(MH \bot CB\) tại \[H\] nên \(\Delta MHB\) vuông tại \[H,\] lại có \[HI\] là đường trung tuyến với cạnh huyền \(MB\) nên \(IH = IM = IB = \frac{1}{2}MB.\)
Vậy \(IO = IM = IH = IB\) nên bốn điểm \[O;{\rm{ }}M;{\rm{ }}H;{\rm{ }}B\] cùng thuộc đường tròn tâm \[I,\] đường kính \(MB.\)
Câu hỏi cùng đoạn
Câu 2:
b) Hai đường thẳng \(MB\) và \(OH\) cắt nhau tại \(E.\) Chứng minh \(\widehat {MHO} = \widehat {MNA}\) và \(ME \cdot MH = BE \cdot HC.\)
⦁ Chứng minh \(\widehat {MHO} = \widehat {MNA}\)
Xét đường tròn ngoại tiếp đi qua bốn điểm \[O;{\rm{ }}M;{\rm{ }}H;{\rm{ }}B\] có \(\widehat {MHO} = \widehat {MBO}\) (hai góc nội tiếp cùng chắn cung \[MO).\]
Xét đường tròn tâm \[O\] có: \(\widehat {MBA} = \widehat {MNA}\) (hai góc nội tiếp cùng chắn cung \[MA)\] hay \(\widehat {MBO} = \widehat {MNA}\)
Do đó: \(\widehat {MHO} = \widehat {MNA}.\)
⦁ Chứng minh \(ME \cdot MH = BE \cdot HC\)
Xét đường tròn ngoại tiếp đi qua bốn điểm \[O;{\rm{ }}M;{\rm{ }}H;{\rm{ }}B\] có \(\widehat {BMO} = \widehat {BHO}\) (hai góc nội tiếp cùng chắn cung \[OB)\]
Tam giác \[MBO\] cân tại \[O\] (do \(OM = OB)\) nên \(\widehat {BMO} = \widehat {MBO}\).
Lại có \(\widehat {MHO} = \widehat {MBO}\) (chứng minh trên)
Suy ra \(\widehat {MHO} = \widehat {BHO}\) nên \[HO\] là tia phân giác của \(\widehat {MHB}\) hay \[ME\] là tia phân giác của \(\widehat {MHB}.\)
Xét \(\Delta MHB\) có \[ME\] là tia phân giác của \(\widehat {MHB}\) nên \(\frac{{ME}}{{BE}} = \frac{{MH}}{{BH}}\) (1)
Xét đường tròn \(\left( O \right)\) có \(AB\) là đường kính và \(M \in \left( O \right)\) nên \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn), do đó \(\widehat {CMB} = 90^\circ \) nên \(\widehat {HMC} + \widehat {HMB} = 90^\circ .\)
Mặt khác, \(\Delta MHB\) vuông tại \(H\) nên \(\widehat {HMB} + \widehat {HBM} = 90^\circ \) (tổng hai góc nhọn trong tam giác vuông).
Suy ra \(\widehat {HMC} = \widehat {HBM}.\)
Xét \(\Delta MHC\) và \(\Delta BHM\) có: \(\widehat {HMC} = \widehat {BHM} = 90^\circ \) và \(\widehat {HMC} = \widehat {HBM}\)
Do đó (g.g), suy ra \(\frac{{MH}}{{BH}} = \frac{{HC}}{{HM}}\) (2)
Từ (1) và (2) suy ra \(\frac{{ME}}{{BE}} = \frac{{HC}}{{HM}}\,\,\left( { = \frac{{MH}}{{BH}}} \right)\) hay \(ME \cdot MH = BE \cdot HC\).
Câu 3:
c) Gọi \(P\) là giao điểm thứ hai của đường tròn \(\left( O \right)\) và đường tròn ngoại tiếp tam giác \(MHC.\) Chứng minh ba điểm \(C,\,\,P,\,\,E\) là ba điểm thẳng hàng.
⦁ Tam giác \[MHC\] vuông tại \[C\] nên ba điểm \[M,{\rm{ }}H,{\rm{ }}C\] nội tiếp đường tròn đường kính \[MC.\]
Mà \[P\] thuộc đường tròn đó nên \(\widehat {MPC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Mặt khác, \[P\] thuộc đường tròn tâm \[O,\] đường kính \[MN\] nên \(\widehat {MPN} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Vậy \(\widehat {MPN} + \widehat {MPC} = 90^\circ + 90^\circ = 180^\circ \) nên \[C,{\rm{ }}P,{\rm{ }}N\] thẳng hàng. (3)
⦁ Xét \(\Delta MHC\) và \(\Delta BMC\) có:
\(\widehat {MHC} = \widehat {BMC} = 90^\circ \) và \(\widehat {MCB}\) là góc chung
Do đó (g.g), suy ra \(\frac{{MH}}{{BM}} = \frac{{HC}}{{MC}}\) hay \(\frac{{HC}}{{MH}} = \frac{{MC}}{{BM}}\).
Tam giác \[BMN\]có \[BO\] là đường cao đồng thời là đường trung tuyến nên \[\Delta BMN\] cân tại \[B\], suy ra \(BM = BN.\)
Do đó từ \(\frac{{HC}}{{MH}} = \frac{{MC}}{{BM}}\) ta có \(\frac{{HC}}{{MH}} = \frac{{MC}}{{BN}}\)
Theo câu b ta có: \(\frac{{ME}}{{BE}} = \frac{{HC}}{{HM}}\) nên \(\frac{{ME}}{{BE}} = \frac{{MC}}{{BN}}\).
Xét đường tròn \(\left( O \right)\) đường kính \(MN\) có \(B \in \left( O \right)\) nên \(\widehat {NBM} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(\widehat {NBE} = 90^\circ .\)
Xét \(\Delta MCE\) và \(\Delta BNE\) có: \(\widehat {CME} = \widehat {NBE} = 90^\circ \) và \(\frac{{ME}}{{BE}} = \frac{{MC}}{{BN}}\)
Do đó (g.g), suy ra \(\widehat {MEC} = \widehat {BEN}\) (hai góc tương ứng).
Ta có: \(\widehat {BEN} + \widehat {CEB} = \widehat {MEC} + \widehat {CEB} = \widehat {MEB} = 180^\circ \) nên ba điểm \[C,{\rm{ }}E,{\rm{ }}N\] thẳng hàng. (4)
Từ (3) và (4) ta có bốn điểm \[C;{\rm{ }}P;{\rm{ }}E;{\rm{ }}N\] thẳng hàng hay \[C;{\rm{ }}P;{\rm{ }}E\] thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
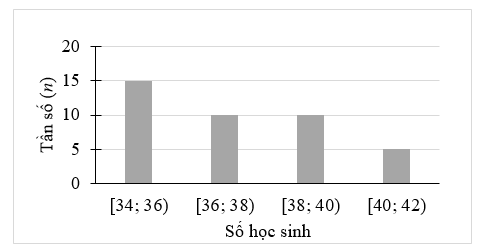
Tần số ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là 5.
Tần số tương đối ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là: \(f = \frac{5}{{40}} \cdot 100\% = 12,5\% .\)
Lời giải
a) Bán kính đáy của lý nước có dạng hình trụ đó là: \(\frac{5}{2} = 2,5{\rm{\;(cm)}}{\rm{.}}\)
Thể tích lượng nước tinh khiết được chứa trong ly bằng thể tích của hình trụ có chiều cao \(10\) cm, và bằng:
\({V_1} = \pi \cdot {\left( {2,5} \right)^2} \cdot 10 = 62,5\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.