Câu hỏi:
12/03/2025 349
(0,5 điểm) Trong buổi thăm quan dã ngoại, mỗi lớp khối 9 được chuẩn bị một tấm bạt hình chữ nhật \(ABCD\) cùng loại, có chiều dài 10 m và chiều rộng 6 m; với \(M,\,\,N\) lần lượt là trung điểm của \[AD,\,\,BC\] (hình 1).
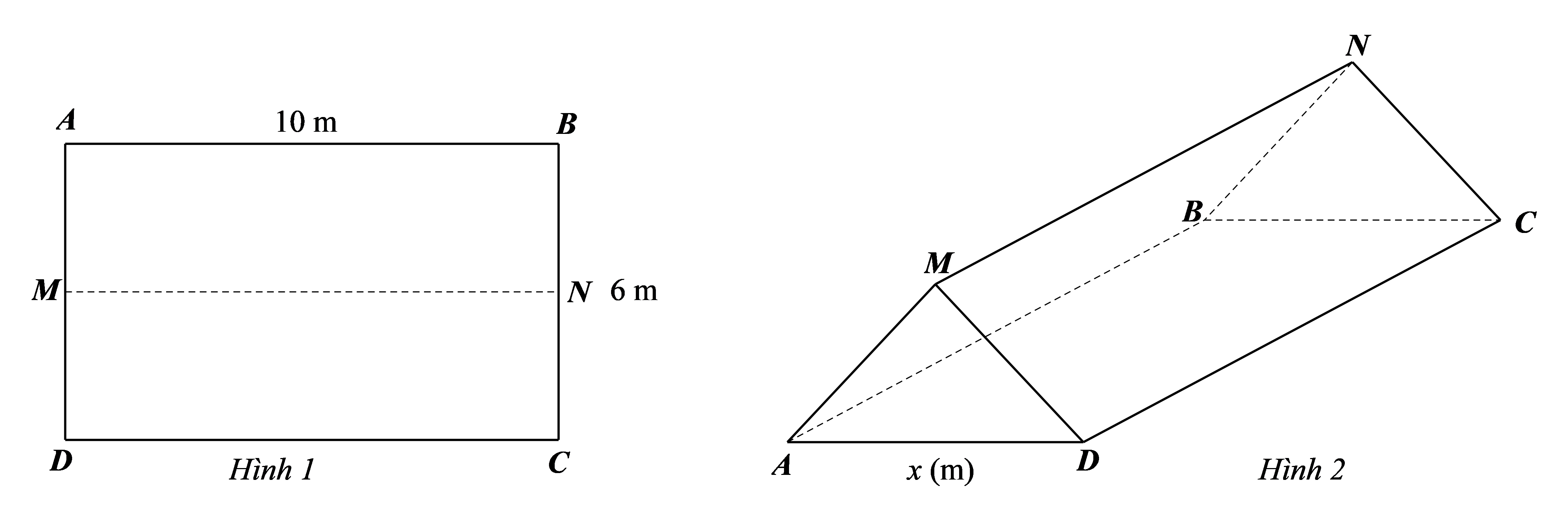
Mỗi lớp sử dụng tấm bạt như trên để dựng thành chiếc lều có dạng hình lăng trụ đứng tam giác (hình 2); hai đáy hình lăng trụ là hai tam giác cân: tam giác \(AMD\) và tam giác \(BNC,\) với độ dài cạnh đáy của hai tam giác cân này là \(x{\rm{\;(m)}}{\rm{.}}\) (Tấm bạt chỉ sử dụng để dựng thành hai mái lều, không trải thành đáy lều). Tìm \(x\) để thể tích không gian trong lều là lớn nhất.
(0,5 điểm) Trong buổi thăm quan dã ngoại, mỗi lớp khối 9 được chuẩn bị một tấm bạt hình chữ nhật \(ABCD\) cùng loại, có chiều dài 10 m và chiều rộng 6 m; với \(M,\,\,N\) lần lượt là trung điểm của \[AD,\,\,BC\] (hình 1).
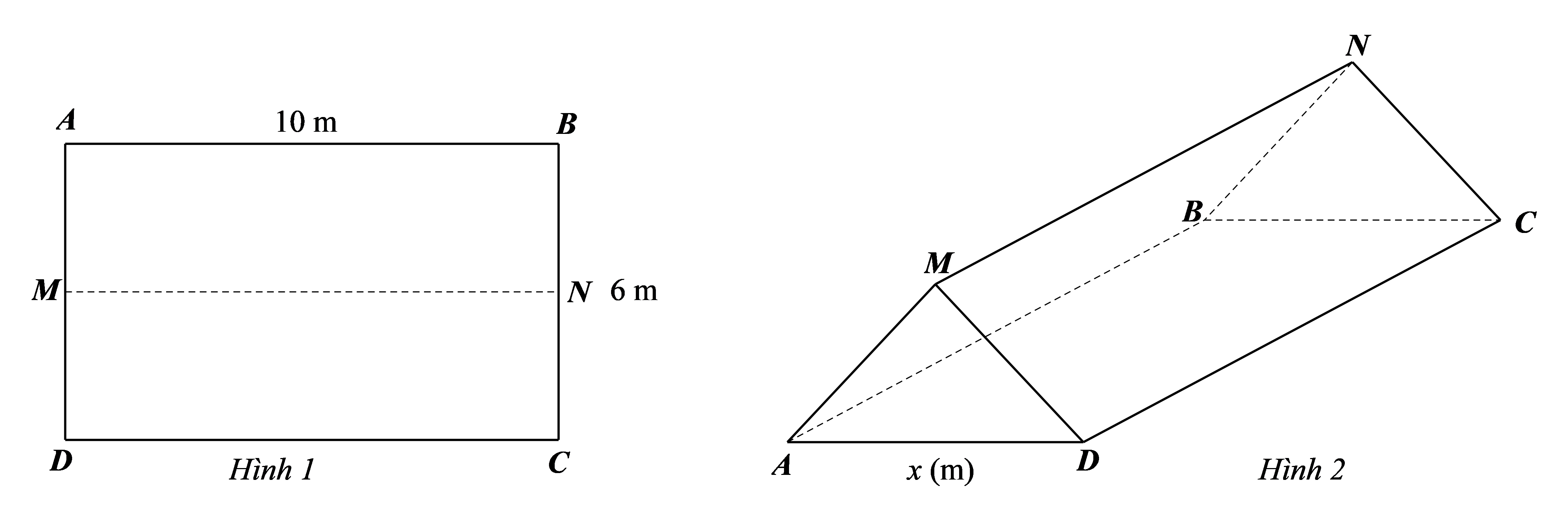
Mỗi lớp sử dụng tấm bạt như trên để dựng thành chiếc lều có dạng hình lăng trụ đứng tam giác (hình 2); hai đáy hình lăng trụ là hai tam giác cân: tam giác \(AMD\) và tam giác \(BNC,\) với độ dài cạnh đáy của hai tam giác cân này là \(x{\rm{\;(m)}}{\rm{.}}\) (Tấm bạt chỉ sử dụng để dựng thành hai mái lều, không trải thành đáy lều). Tìm \(x\) để thể tích không gian trong lều là lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì \(M\) là trung điểm của đoạn \(AD\) trên tấm bạt hình chữ nhật \(ABCD\) (hình 1) nên \(MA = MD = \frac{1}{2}AD = \frac{6}{2} = 3{\rm{\;(m)}}{\rm{.}}\)
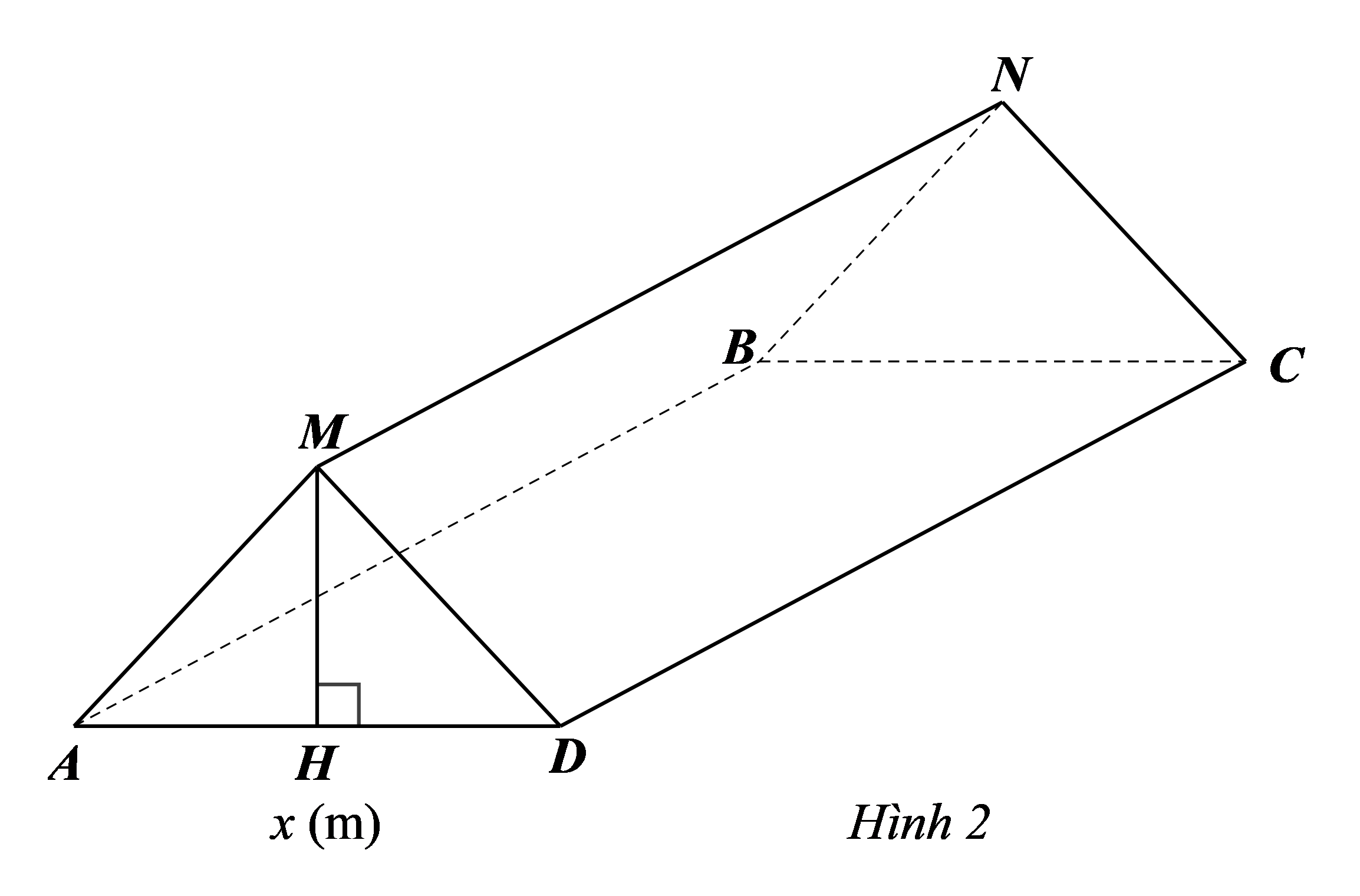
Kẻ đường cao \(MH\) \(\left( {H \in AD} \right)\) của tam giác \(AMD.\) Khi đó đường cao \(MH\) của \(\Delta AMD\) cân tại \(M\) đồng thời là đường trung tuyến nên \(H\) là trung điểm của \(AD,\) do đó \(HD = \frac{{AD}}{2} = \frac{x}{2}\) \[\left( {0 < x < 6} \right).\]
Xét \(\Delta MHD\) vuông tại \[H,\] theo định lí Pythagore, ta có: \(M{D^2} = M{H^2} + H{D^2}\)
Suy ra \[MH = \sqrt {M{D^2} - H{D^2}} = \sqrt {{3^2} - {{\left( {\frac{x}{2}} \right)}^2}} = \sqrt {9 - \frac{{{x^2}}}{4}} = \frac{{\sqrt {36 - {x^2}} }}{2}{\rm{\;(m)}}{\rm{.}}\]
Diện tích \(\Delta AMD\) là: \({S_{\Delta AMD}} = \frac{1}{2} \cdot AD \cdot MH = \frac{1}{2} \cdot x \cdot \frac{{\sqrt {36 - {x^2}} }}{2} = \frac{{x\sqrt {36 - {x^2}} }}{4}{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Thể tích hình lăng trụ đứng tam giác \[AMD.BNC\] là:
\(V = {S_{\Delta AMD}} \cdot MN = \frac{{x\sqrt {36 - {x^2}} }}{4} \cdot 10 = \frac{5}{2}x\sqrt {36 - {x^2}} {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Đặt \[P = \frac{5}{2}x\sqrt {36 - {x^2}} ,\] suy ra \[{P^2} = \frac{{25}}{4}{x^2}\left( {36 - {x^2}} \right)\mathop \le \limits^{BDT\,\,Cauchuy} \frac{{25}}{4} \cdot {\left( {\frac{{{x^2} + 36 - {x^2}}}{2}} \right)^2} = 2025.\]
Suy ra \(P \le 45\).
Đẳng thức xảy ra khi và chỉ khi \({x^2} = 36 - {x^2}\) hay \(2{x^2} = 36\) nên \({x^2} = 18\), tức là \(x = 3\sqrt 2 \) (do \[0 < x < 6).\]
Vậy để thể tích không gian trong lều lớn nhất thì độ dài đoạn \(AD = 3\sqrt 2 \) (m).
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
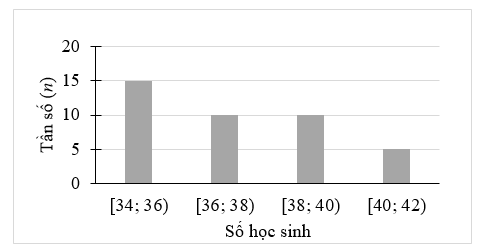
Tần số ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là 5.
Tần số tương đối ghép nhóm của nhóm \(\left[ {40;\,\,42} \right)\) là: \(f = \frac{5}{{40}} \cdot 100\% = 12,5\% .\)
Lời giải
a) Bán kính đáy của lý nước có dạng hình trụ đó là: \(\frac{5}{2} = 2,5{\rm{\;(cm)}}{\rm{.}}\)
Thể tích lượng nước tinh khiết được chứa trong ly bằng thể tích của hình trụ có chiều cao \(10\) cm, và bằng:
\({V_1} = \pi \cdot {\left( {2,5} \right)^2} \cdot 10 = 62,5\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa