Câu 5-6 (1,5 điểm) Biên độ nhiệt là khoảng cách chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất trong cùng một khoảng thời gian nhất định (một ngày, một tháng, một năm, …) của cùng một vùng địa lí. Biểu đồ cột kép dưới đây biểu diễn nhiệt độ (độ C) các ngày trong một tuần tại Thành phố Hồ Chí Minh.
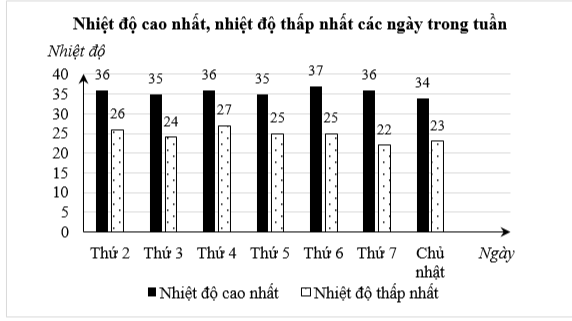
1) Trong tuần này, ngày có biên độ nhiệt lớn nhất của thành phố Hồ Chí Minh là thứ mấy?
Câu 5-6 (1,5 điểm) Biên độ nhiệt là khoảng cách chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất trong cùng một khoảng thời gian nhất định (một ngày, một tháng, một năm, …) của cùng một vùng địa lí. Biểu đồ cột kép dưới đây biểu diễn nhiệt độ (độ C) các ngày trong một tuần tại Thành phố Hồ Chí Minh.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dựa vào biểu đồ cột kép, ta có biên độ nhiệt của các ngày trong tuần là:
Thứ 2: \[36 - 26 = 10,\] thứ 3: \[35 - 24 = 11,\] thứ 4: \[36 - 27 = 9;\] thứ 5: \[35 - 25 = 10;\]
Thứ 6: \[37 - 25 = 12;\] thứ 7: \[36 - 22 = 14;\] chủ nhật: \[34 - 23 = 11.\]
Vậy ngày có biên độ nhiệt lớn nhất trong tuần của thành phố Hồ Chí Minh là thứ 7.
Câu hỏi cùng đoạn
Câu 2:
2) Chọn ngẫu nhiên một ngày trong tuần, tính xác suất của các biến cố sau:
A: “Ngày được chọn có nhiệt độ cao nhất không quá 35 độ C”.
B: “Ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C”.
A: “Ngày được chọn có nhiệt độ cao nhất không quá 35 độ C”.
B: “Ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C”.
Giải bởi Vietjack
Ta có số ngày có nhiệt độ cao không quá 35 độ C là 3 (ngày).
Suy ra số phần tử của biến cố A là 3.
Xác suất để ngày được chọn có nhiệt độ cao nhất không quá 35 độ C là \(\frac{3}{7}\).
Có số ngày có biên độ nhiệt nhỏ hơn 12 độ C là 5 (ngày).
Suy ra số phần tử của biến cố B là 5.
Xác suất để ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C là \(\frac{5}{7}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1) Phương trình \[2{x^2} - 5x + 1 = 0\] có \[a = 2\,;\,\,b = - 5\,;\,\,c = 1\] nên ta có:
\[\Delta \; = \;{\left( { - 5} \right)^2} - \;4 \cdot 2 \cdot 1 = \;25 - \;8 = \;17 > \;0\] nên phương trình có hai nghiệm phân biệt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1) Chiều rộng của khu vườn hình chữ nhật sau khi mở rộng là:
\[30 + x + x = 30 + 2x\,\,\left( {\rm{m}} \right)\]
Chiều dài của khu vườn hình chữ nhật sau khi mở rộng là:
\[70 + x + x = 70 + 2x\,\,\left( {\rm{m}} \right)\]
Diện tích của khu vườn hình chữ nhật sau khi mở rộng là:
\[\left( {30 + 2x} \right)\left( {70 + 2x} \right)\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Vậy biểu thức \[S\] biểu diễn theo \[x\] là \[S = \left( {30 + 2x} \right)\left( {70 + 2x} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập