Địa y là một dạng kết hợp giữa nấm và một loại sinh vật có thể quang hợp (có thể là tảo lục hay khuẩn lam) trong một mối quan hệ cộng sinh. Địa y tồn tại ở một số môi trường khắc nghiệt nhất thế giới như đài nguyên bắc cực, sa mạc, bờ đá. Chúng rất phong phú trên các lá và cành cây tại rừng mưa và rừng gỗ, trên đá, cả trên tường gạch và đất. Nóc của nhiều tòa nhà cũng có địa y mọc. Địa y rất phổ biến và có thể sống lâu; tuy nhiên, nhiều loại địa y dễ bị tổn thương khi thay đổi thời tiết đột ngột, chúng có thể được các nhà khoa học dùng để đo mức độ ô nhiễm không khí, hay hủy hoại tầng ozone.
Kết quả của sự nóng dần lên của trái đất làm băng tan trên các dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.
Mối quan hệ giữa đường kính d, tính bằng mi-li-mét ( mm ), của hình tròn và tuổi t của Địa y có thể biểu diễn tương đối theo công thức: \({\rm{d}} = 7\sqrt {{\rm{t}} - 12} \), với \(t \ge 12\)
a) Em hãy sử dụng công thức trên để tính đường kính của một nhóm Địa y, 16 năm sau khi băng tan.
b) An đo đường kính của một số nhóm địa y và thấy có số đo là 35 mm. Đối với kết quả trên thì băng đã tan cách đó bao nhiêu năm?
Địa y là một dạng kết hợp giữa nấm và một loại sinh vật có thể quang hợp (có thể là tảo lục hay khuẩn lam) trong một mối quan hệ cộng sinh. Địa y tồn tại ở một số môi trường khắc nghiệt nhất thế giới như đài nguyên bắc cực, sa mạc, bờ đá. Chúng rất phong phú trên các lá và cành cây tại rừng mưa và rừng gỗ, trên đá, cả trên tường gạch và đất. Nóc của nhiều tòa nhà cũng có địa y mọc. Địa y rất phổ biến và có thể sống lâu; tuy nhiên, nhiều loại địa y dễ bị tổn thương khi thay đổi thời tiết đột ngột, chúng có thể được các nhà khoa học dùng để đo mức độ ô nhiễm không khí, hay hủy hoại tầng ozone.
Kết quả của sự nóng dần lên của trái đất làm băng tan trên các dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.
Mối quan hệ giữa đường kính d, tính bằng mi-li-mét ( mm ), của hình tròn và tuổi t của Địa y có thể biểu diễn tương đối theo công thức: \({\rm{d}} = 7\sqrt {{\rm{t}} - 12} \), với \(t \ge 12\)
a) Em hãy sử dụng công thức trên để tính đường kính của một nhóm Địa y, 16 năm sau khi băng tan.
b) An đo đường kính của một số nhóm địa y và thấy có số đo là 35 mm. Đối với kết quả trên thì băng đã tan cách đó bao nhiêu năm?
Câu hỏi trong đề: 33 bài tập Căn thức có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Thay \({\rm{t}} = 16\) vào công thức \({\rm{d}} = 7\sqrt {{\rm{t}} - 12} \), ta được: \({\rm{d}} = 7 \cdot \sqrt {16 - 12} = 7.2 = 14\;{\rm{mm}}\).
Vậy sau 16 năm thì đường kính của một nhóm Địa y là 14 mm.
b) Thay \({\rm{d}} = 35\) vào công thức \({\rm{d}} = 7\sqrt {{\rm{t}} - 12} \), ta được: \(7\sqrt {t - 12} = 35 \Rightarrow \sqrt {t - 12} = 5 \Rightarrow t - 12 = 25 \Rightarrow t = 37\) (năm)
Vậy băng tan cách đó: \(37 + 12 = 49\) (năm)
Vậy sau 16 năm thì đường kính của một nhóm Địa y là 14 mm.
b) Thay \({\rm{d}} = 35\) vào công thức \({\rm{d}} = 7\sqrt {{\rm{t}} - 12} \), ta được: \(7\sqrt {t - 12} = 35 \Rightarrow \sqrt {t - 12} = 5 \Rightarrow t - 12 = 25 \Rightarrow t = 37\) (năm)
Vậy băng tan cách đó: \(37 + 12 = 49\) (năm)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Thay \({\rm{L}} = 2 + \sqrt 3 ;{\rm{g}} = 9,81\) vào công thức \({\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} \), ta được:\({\rm{T}} = 2\pi \sqrt {\frac{{2 + \sqrt 3 }}{{9,81}}} \approx 3,88{\rm{ (gi\^a y)}}{\rm{. }}\)
Vậy chu kỳ đong đưa dài 3,88 giây.
b) Thay \({\rm{T}} = 4;{\rm{g}} = 9,81\) vào công thức \({\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} \), ta được:
\(4 = 2\pi \cdot \sqrt {\frac{{\rm{L}}}{{9,81}}} \Rightarrow \sqrt {\frac{{\rm{L}}}{{9,81}}} = \frac{2}{\pi } \Rightarrow \frac{{\rm{L}}}{{9,81}} = {\left( {\frac{2}{\pi }} \right)^2} \Rightarrow {\rm{L}} = 9,81.{\left( {\frac{2}{\pi }} \right)^2} \approx 4\;{\rm{m}}\)
Vậy phải làm một dây đu dài 4 m.
Vậy chu kỳ đong đưa dài 3,88 giây.
b) Thay \({\rm{T}} = 4;{\rm{g}} = 9,81\) vào công thức \({\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} \), ta được:
\(4 = 2\pi \cdot \sqrt {\frac{{\rm{L}}}{{9,81}}} \Rightarrow \sqrt {\frac{{\rm{L}}}{{9,81}}} = \frac{2}{\pi } \Rightarrow \frac{{\rm{L}}}{{9,81}} = {\left( {\frac{2}{\pi }} \right)^2} \Rightarrow {\rm{L}} = 9,81.{\left( {\frac{2}{\pi }} \right)^2} \approx 4\;{\rm{m}}\)
Vậy phải làm một dây đu dài 4 m.
Lời giải
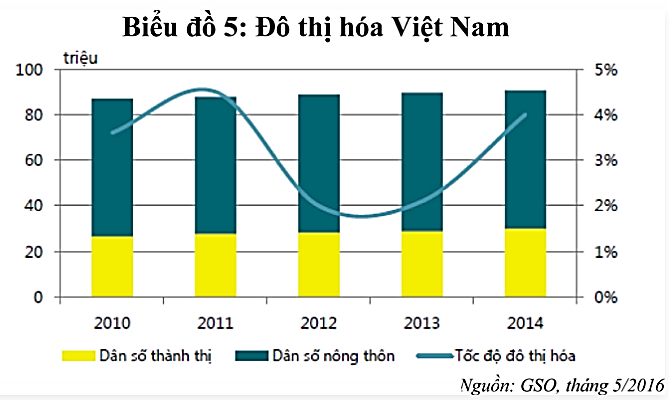
a) Thay \({{\rm{P}}_t} = 91703,8;{{\rm{P}}_0} = 90728,9\) vào công thức \(\overline {\rm{r}} = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{{{\rm{P}}_0}}}} - 1\), ta được:\(\bar r = \sqrt {\frac{{91703,8}}{{90728,9}}} - 1 = 0,0054 = 0,54\% \)
Vậy tốc độ tăng trương dân số bình quân hàng năm trong giai đoạn trên của Việt Nam là \(0,54\% \).
b) Thay \(r = 0,0054;{P_0} = 91703,8\) vào công thức \(\bar r = \sqrt {\frac{{{P_t}}}{{{P_0}}}} - 1\), ta được:
\(0,054 = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} - 1 \Rightarrow \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} = 1,0054 \Rightarrow \frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}} = {(1,0054)^2}\)
\( \Rightarrow {{\rm{P}}_{\rm{t}}} = {(1,0054)^2} \cdot 91703,8 \approx 92199,00052\)
Vậy ước tính số dân Việt Nam vào năm 2016 là 92199,00052 ngàn người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo