Sử dụng phương pháp nhân tử Lagrange giải bài toán tìm cực trị có điều kiện, ta biết rằng hàm Lagrange L có điểm dừng M₀ (x₀, y₀, -12) và L’_xx = -2 λ; L_yx’’ = 0 ; L’’_yy = -4 λ; g_y’ = 1. Khi đó tại điểm (x₀, y₀), hàm số với điều kiện đã cho:

Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3x² + y² = 28. Hàm Lagrange L = 3x + 2y + λ (28 – 3x² – y²) có các đạo hàm riêng cấp 1 L_x’ = 3 – 6 λx; L_x’ = 2 – 2 λy. Hàm số L có điểm dừng là M₀ (x₀, y₀, λ₀) với λ₀ = _và:

Với hàm sản xuất dạng Cobb – Douglas Q=a.Kα Lβ(a, α, β>0) , theo quy luật lợi ích cận biên giảm dần các tham số α, β phải thỏa mãn điều kiện:

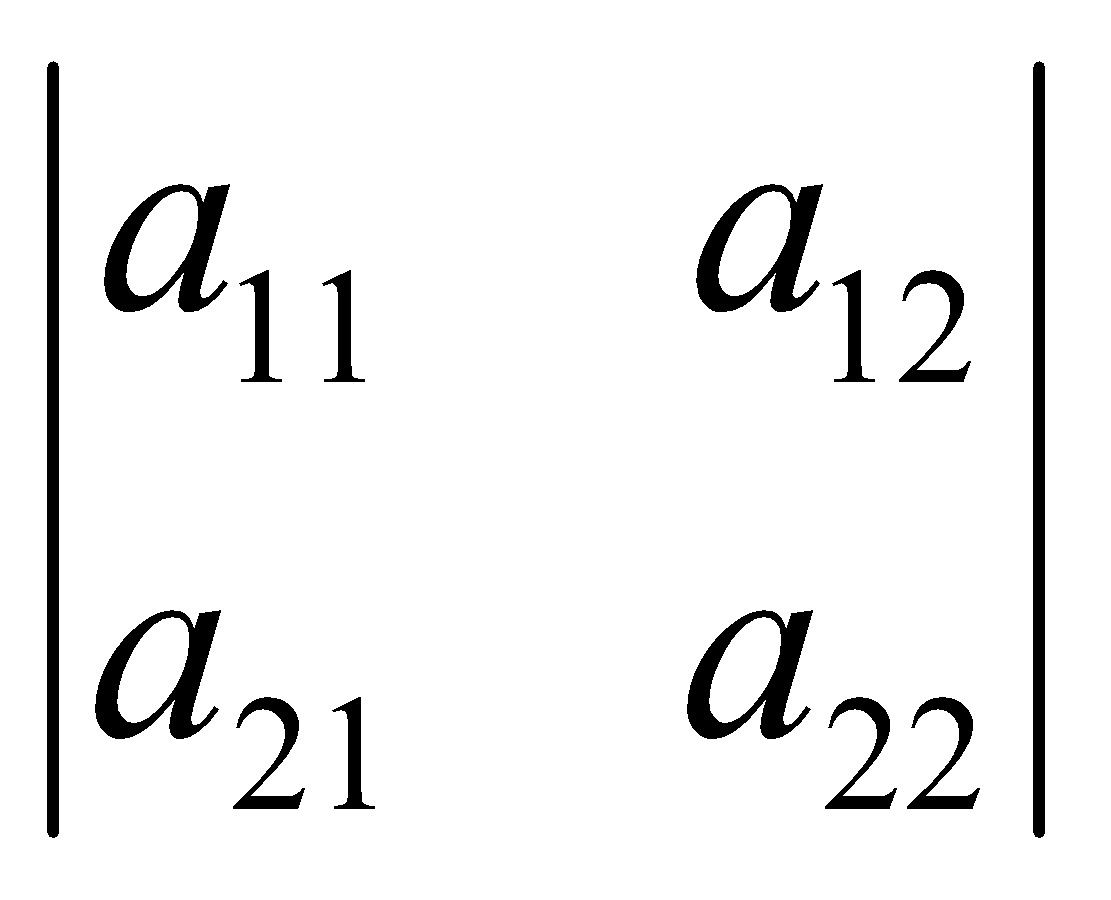Xét hàm số 2 biến số w = f(x, y). Ký hiệu: D = _{= a11}. a₂₂ – a₁₂. a₂₁ với a₁₁, a₁₂, a₂₁, a₂₂ lần lượt là giá trị của các đạo hàm riêng cấp 2 w_xx’’, w_xy’’, w_yy’’ tính tại điểm dừng M₀ (x₀, y₀). Khi đó nếu D>0 thì theo điều kiện đủ của cực trị, điểm M₀ (x₀, y₀):

Cho hàm số y=sin(cosx). Đạo hàm y′ là :

Khi giả bài toán tìm cực trị của hàm số w = x² + y² với điều kiện ràng buộc là phương trình 3x + 2y = 26, hàm Lagrange L có điểm dừng là M₀ (x₀, y₀, λ₀) với y₀ = λ₀ và x₀ có giá trị là:

Cho y = (3x – 2) . e^-2x. Giá trị của y’’(1) là: