PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[y = \frac{{{x^2} + 2x - 1}}{{x - 1}}\] có đồ thị \[\left( C \right)\].
a) Hàm số có 2 điểm cực trị.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[y = \frac{{{x^2} + 2x - 1}}{{x - 1}}\] có đồ thị \[\left( C \right)\].
a) Hàm số có 2 điểm cực trị.
Quảng cáo
Trả lời:
a) Đúng. Hàm số\[y = \frac{{{x^2} + 2x - 1}}{{x - 1}} = x + 3 + \frac{2}{{x - 1}}\].
Tập xác định \[D = \left( { - \infty \,;1} \right) \cup \left( {1\,; + \infty } \right)\], đạo hàm \[y' = 1 - \frac{2}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 2 \\x = 1 - \sqrt 2 \end{array} \right.\].
Câu hỏi cùng đoạn
Câu 2:
b) Hàm số nghịch biến trên khoảng \[\left( {0\,;2} \right)\].
b) Hàm số nghịch biến trên khoảng \[\left( {0\,;2} \right)\].
b) Sai. Vì hàm số không xác định tại \(x = 1 \in \left( {0\,;2} \right)\).
Câu 3:
c) Đồ thị \[\left( C \right)\] có tiệm cận đứng là đường thẳng có phương trình \(x = 1\).
c) Đồ thị \[\left( C \right)\] có tiệm cận đứng là đường thẳng có phương trình \(x = 1\).
c) Đúng. Vì \[\mathop {\lim }\limits_{x \to {1^ + }} \left( {x + 3 + \frac{2}{{x - 1}}} \right) = + \infty \] nên đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số
Câu 4:
d) \[M\] là điểm bất kì thuộc đồ thị \[\left( C \right)\]. Tích khoảng cách từ \[M\] đến tiệm cận đứng và tiệm cận xiên của đồ thị \[\left( C \right)\] bằng \[\sqrt 2 \].
d) \[M\] là điểm bất kì thuộc đồ thị \[\left( C \right)\]. Tích khoảng cách từ \[M\] đến tiệm cận đứng và tiệm cận xiên của đồ thị \[\left( C \right)\] bằng \[\sqrt 2 \].
d) Đúng. Giả sử \[M\left( {{x_0};{x_0} + 3 + \frac{2}{{{x_0} - 1}}} \right)\] với \[{x_0} \ne 1\] là điểm bất kỳ thuộc \[\left( C \right)\].
+) Khoảng cách từ \[M\] tới tiệm cận đứng \[x = 1\] là \[\left| {{x_0} - 1} \right|\].
+) Khoảng cách từ \[M\] tới tiệm cận xiên \[y = x + 3 \Leftrightarrow x - y + 3 = 0\] là
\[\frac{{\left| {{x_0} - \left( {{x_0} + 3 + \frac{2}{{{x_0} - 1}}} \right) + 3} \right|}}{{\sqrt 2 }} = \frac{{\left| {\frac{2}{{{x_0} - 1}}} \right|}}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{{\left| {{x_0} - 1} \right|}}\].
Tích khoảng cách từ \[M\] tới tiệm cận đứng và tiệm cận xiên là \[\left| {{x_0} - 1} \right| \cdot \frac{{\sqrt 2 }}{{\left| {{x_0} - 1} \right|}} = \sqrt 2 \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(6,4\).
Số tiền cả vốn và lãi ông An phải trả cho ngân hàng sau 1 năm là \(200\left( {1 + 8\% } \right) = 216\) (triệu đồng).
Số cổ phiếu ông An mua là: \(200\,000\,000:50\,000 = 4\,000\) (cổ phiếu).
Số tiền ông An bán cổ phiếu là \(4\,000 \cdot 55\,600 = 222\,400\,000\) (đồng) \( = 222,4\) (triệu đồng).
Số tiền còn lại của ông An là \(222,4 - 216 = 6,4\) (triệu đồng).
Lời giải
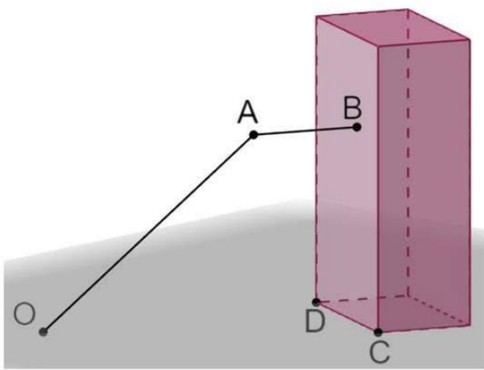
a) Đúng. Ta có \(OA = \sqrt {{{300}^2} + {{\left( { - 400} \right)}^2} + {{100}^2}} = \sqrt {260000} = 100\sqrt {26} \approx 509,9\, > 250\) nên radar không thể phát hiện UAV khi UAV ở vị trí \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.