Câu hỏi:
23/05/2025 119
Trong giờ thể dục học về kỹ thuật chuyền bóng hơi, Bình và An tập chuyền bóng cho nhau. Ở một động tác Bình chuyền bóng cho An, quả bóng bay lên cao nhưng lại lệch sang bên trái của An và rơi xuống vị trí cách chỗ An đứng \[0,5\,{\rm{m}}\] và cách chỗ Bình \[4,5\,{\rm{m}}\]. Chọn hệ trục tọa độ \[Oxyz\] sao cho gốc tọa độ \[O\] tại vị trí của Bình, vị trí của An nằm trên tia \[Ox\] và mặt phẳng \[Oxy\] là mặt đất (tham khảo hình vẽ).
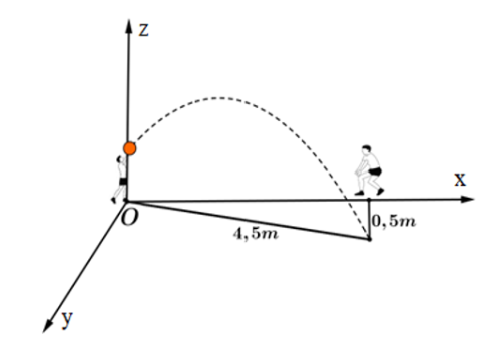
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng \[\left( \alpha \right):x + by + cz + d = 0\] và \[\left( \alpha \right)\] vuông góc với mặt đất. Khi đó, giá trị của \[ - 5{b^2} - {c^2} + 3{d^2}\] bằng bao nhiêu?
Trong giờ thể dục học về kỹ thuật chuyền bóng hơi, Bình và An tập chuyền bóng cho nhau. Ở một động tác Bình chuyền bóng cho An, quả bóng bay lên cao nhưng lại lệch sang bên trái của An và rơi xuống vị trí cách chỗ An đứng \[0,5\,{\rm{m}}\] và cách chỗ Bình \[4,5\,{\rm{m}}\]. Chọn hệ trục tọa độ \[Oxyz\] sao cho gốc tọa độ \[O\] tại vị trí của Bình, vị trí của An nằm trên tia \[Ox\] và mặt phẳng \[Oxy\] là mặt đất (tham khảo hình vẽ).
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng \[\left( \alpha \right):x + by + cz + d = 0\] và \[\left( \alpha \right)\] vuông góc với mặt đất. Khi đó, giá trị của \[ - 5{b^2} - {c^2} + 3{d^2}\] bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \( - 400\).
Quả bóng rơi xuống tại điểm \[A\left( {\sqrt {20} ;0,5;0} \right)\].
Mặt phẳng \[\left( \alpha \right):x + by + cz + d = 0\] đi qua \[O\] nên \[d = 0\], điểm \[A\left( {\sqrt {20} ;0,5;0} \right)\] thuộc \[\left( \alpha \right)\] nên có \[\sqrt {20} + 0,5b = 0 \Leftrightarrow b = - 4\sqrt 5 \].
Mặt khác \[\left( \alpha \right)\] vuông góc với mặt đất nên \[{\overrightarrow n _{\left( \alpha \right)}} \bot {\overrightarrow n _{\left( {Oxy} \right)}} \Leftrightarrow {\overrightarrow n _{\left( \alpha \right)}} \cdot \overrightarrow k = 0 \Leftrightarrow c = 0\].
Vậy mặt phẳng \[\left( \alpha \right)\] có phương trình là \[\left( \alpha \right):x - 4\sqrt 5 y = 0\].
Khi đó, \[ - 5{b^2} - {c^2} + 3{d^2} = - 400\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 48,5.
Ta có \[x + 120 + y + 70 + 60 = 400 \Leftrightarrow x + y = 150\].
Nhận thấy \[{Q_3}\] thuộc nhóm \[\left[ {60;80} \right)\].
\[{Q_3} = 60 + \frac{{\frac{{400 \cdot 3}}{4} - \left( {x + 120 + y} \right)}}{{70}} \cdot 20 = 60 + \frac{{300 - 270}}{{70}} \cdot 20 = \frac{{480}}{7}\,\,\,\left( {{\rm{do}}\,x + y = 150} \right)\]
\[{Q_3} - {Q_1} = \frac{{845}}{{21}} \Leftrightarrow {Q_1} = {Q_3} - \frac{{845}}{{21}} \Leftrightarrow {Q_1} = \frac{{85}}{3}\].
Suy ra \[{Q_1}\] thuộc nhóm \[\left[ {20;40} \right)\].
\[{Q_1} = 20 + \frac{{100 - x}}{{120}} \cdot 20 \Leftrightarrow \frac{{85}}{3} = 20 + \frac{{100 - x}}{6} \Leftrightarrow x = 50 \Rightarrow y = 100\].
Chọn giá trị đại diện cho các nhóm ta có bảng sau
Vậy thời gian học trung bình của các học sinh trong nhóm là
\[\frac{{50 \cdot 10 + 120 \cdot 30 + 100 \cdot 50 + 70 \cdot 70 + 60 \cdot 90}}{{400}} = 48,5\].
Lời giải
a) Đúng. Thay \[t = 4\] vào hàm \[{P'_A}\left( t \right) = - \frac{1}{2}{t^2} + 2t + 8\] ta được:
\[{P'_A}\left( 4 \right) = - \frac{1}{2} \cdot 16 + 2 \cdot 4 + 8 = 8\](ngàn người).
Vậy tốc độ gia tăng dân số của khu vực \[A\] với \[t = 4\] là 8 000.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải