Câu hỏi:
23/05/2025 36
Tại một khu trung tâm dữ liệu, kỹ sư IT cần kiểm tra kết nối giữa các máy chủ trong hệ thống gồm các trạm \(A,\,B,\,C,\,D,\,E.\) Các tuyến cáp quang nối giữa các trạm được biểu diễn trong sơ đồ sau, với con số ghi trên mỗi tuyến là chiều dài dây cáp (đơn vị: km).
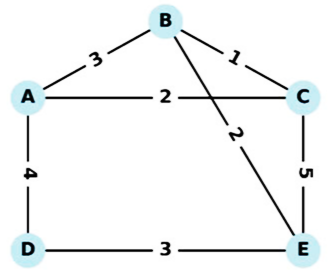
Kỹ sư cần thực hiện một hành trình bắt đầu từ một trạm bất kì, đi qua tất cả các tuyến cáp ít nhất một lần, và kết thúc tại đúng trạm khởi hành, nhằm đảm bảo toàn bộ hệ thống được kiểm tra. Tổng chiều dài đường đi ngắn nhất mà kỹ sư cần di chuyển là bao nhiêu kilômét?
Tại một khu trung tâm dữ liệu, kỹ sư IT cần kiểm tra kết nối giữa các máy chủ trong hệ thống gồm các trạm \(A,\,B,\,C,\,D,\,E.\) Các tuyến cáp quang nối giữa các trạm được biểu diễn trong sơ đồ sau, với con số ghi trên mỗi tuyến là chiều dài dây cáp (đơn vị: km).
Kỹ sư cần thực hiện một hành trình bắt đầu từ một trạm bất kì, đi qua tất cả các tuyến cáp ít nhất một lần, và kết thúc tại đúng trạm khởi hành, nhằm đảm bảo toàn bộ hệ thống được kiểm tra. Tổng chiều dài đường đi ngắn nhất mà kỹ sư cần di chuyển là bao nhiêu kilômét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 24.
+) Đường đi ảo giữa hai đỉnh là đường đi ngắn nhất giữa hai đỉnh đó.
+) Ý tưởng giải bài toán là tạo ra tất cả các đỉnh bậc chẵn bằng cách thêm đường đi ảo. Khi đó sẽ có chu trình Euler (tức là đường đi từ 1 đỉnh qua tất cả các cạnh đúng 1 lần và trở về đỉnh ban đầu).
Áp dụng:
+) Trước tiên, ta thấy tổng độ dài tất các các con đường là: 3 + 1 + 5 + 3 + 4 + 2 + 2 = 20.
+) Vì đồ thị có đúng 4 đỉnh bậc lẻ A, B, C, E nên có 3 cách ghép cặp đỉnh để xây dựng đường đi ảo giữa các cặp đỉnh đó như sau:
Cách 1: A - B và C - E: Tổng độ dài đường đi ảo là: 3 + 5 = 8.
Cách ghép này cho ta chu trình Euler có độ dài 20 + 8 = 28.
Cách 2: A - C và B - E: Tổng độ dài đường đi ảo là: 2 + 2 = 4.
Cách ghép này cho ta chu trình Euler có độ dài 20 + 4 = 24.
Cách 3: A - E và B - C: Tổng độ dài đường đi ảo là: 5 + 1 = 6.
Cách ghép này cho ta chu trình Euler có độ dài 20 + 6 = 26.
Vậy đáp án của bài toán là 24 km.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết)
Đã bán 986
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
a) Một vectơ chỉ phương của đường thẳng \[AB\] là \(\vec u = \left( {0;5;1} \right)\).
a) Một vectơ chỉ phương của đường thẳng \[AB\] là \(\vec u = \left( {0;5;1} \right)\).
Xem đáp án »
23/05/2025
73
Câu 5:
Một người tham gia trò chơi với \[3\]hộp quà đặc biệt: Hộp màu vàng có \[2\] điện thoại iPhone và \[3\] tai nghe, hộp màu bạc có \[4\] điện thoại iPhone và \[1\] tai nghe, hộp màu đồng có \[3\] điện iPhone và \[2\] tai nghe. Luật chơi được thực hiện qua hai bước sau:
Bước 1. Người chơi chọn ngẫu nhiên \[1\] hộp.
Bước 2. Từ hộp đã chọn, người chơi lấy ngẫu nhiên \[1\] món quà:
- Nếu quà là điện thoại iPhone, người chơi được giữ nó và lấy thêm \[1\] quà nữa từ cùng hộp.
- Nếu quà là tai nghe, trò chơi kết thúc.
Biết rằng người chơi lấy được \[2\] điện thoại iPhone, tính xác suất để người đó lấy từ hộp màu bạc (làm tròn kết quả đến hàng phần mười).
Một người tham gia trò chơi với \[3\]hộp quà đặc biệt: Hộp màu vàng có \[2\] điện thoại iPhone và \[3\] tai nghe, hộp màu bạc có \[4\] điện thoại iPhone và \[1\] tai nghe, hộp màu đồng có \[3\] điện iPhone và \[2\] tai nghe. Luật chơi được thực hiện qua hai bước sau:
Bước 1. Người chơi chọn ngẫu nhiên \[1\] hộp.
Bước 2. Từ hộp đã chọn, người chơi lấy ngẫu nhiên \[1\] món quà:
- Nếu quà là điện thoại iPhone, người chơi được giữ nó và lấy thêm \[1\] quà nữa từ cùng hộp.
- Nếu quà là tai nghe, trò chơi kết thúc.
Biết rằng người chơi lấy được \[2\] điện thoại iPhone, tính xác suất để người đó lấy từ hộp màu bạc (làm tròn kết quả đến hàng phần mười).
Xem đáp án »
23/05/2025
48
Câu 6:
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty đang triển khai chiến dịch quảng cáo sản phẩm mới. Số tiền đầu tư quảng cáo là A (triệu đồng). Theo kết quả nghiên cứu thị trường, số lượng sản phẩm bán ra (đơn vị: sản phẩm) phụ thuộc vào chi phí quảng cáo theo hàm số \[q\left( A \right) = 1000 + \frac{{1013}}{5}\ln \left( {1 + A} \right)\].
Biết rằng, chi phí sản xuất mỗi sản phẩm là 10 triệu đồng và giá bán mỗi sản phẩm là 20 triệu đồng. Giá trị lợi nhuận tối đa mà công ty có thể đạt được là bao nhiêu tỉ đồng (làm tròn kết quả đến hàng phần mười)?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty đang triển khai chiến dịch quảng cáo sản phẩm mới. Số tiền đầu tư quảng cáo là A (triệu đồng). Theo kết quả nghiên cứu thị trường, số lượng sản phẩm bán ra (đơn vị: sản phẩm) phụ thuộc vào chi phí quảng cáo theo hàm số \[q\left( A \right) = 1000 + \frac{{1013}}{5}\ln \left( {1 + A} \right)\].
Biết rằng, chi phí sản xuất mỗi sản phẩm là 10 triệu đồng và giá bán mỗi sản phẩm là 20 triệu đồng. Giá trị lợi nhuận tối đa mà công ty có thể đạt được là bao nhiêu tỉ đồng (làm tròn kết quả đến hàng phần mười)?
Xem đáp án »
23/05/2025
44
Câu 7:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Tìm nguyên hàm của hàm số \[f\left( x \right) = \frac{1}{{5x - 12}}\].
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Tìm nguyên hàm của hàm số \[f\left( x \right) = \frac{1}{{5x - 12}}\].
Xem đáp án »
23/05/2025
38
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận