Chào mừng tháng Thanh niên. Đoàn trường THPT X tổ chức cải tạo một khoảng đất trong khuôn viên nhà trường có hình dạng là một đường tròn có đường kính \(8\,{\rm{m}}\). Để tăng tính thẩm mỹ, khi thực hiện cải tạo đã chia mảnh đất đó thành hai phần bằng một đường cong là một phần của đồ thị hàm số bậc ba \(y = f\left( x \right)\), phần gạch chéo dùng để trồng hoa và phần còn lại dùng để trồng cỏ, được mô hình hóa trong hệ trục \(Oxy\) như hình vẽ dưới đây.
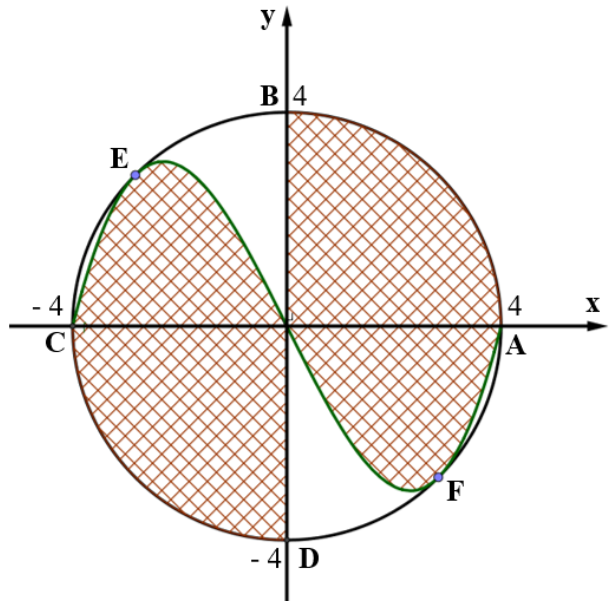
Biết đồ thị hàm số bậc ba \(y = f\left( x \right)\) có tâm đối xứng trùng với gốc tọa độ; đi qua các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung và đi qua các giao điểm của đường tròn với trục \(Ox\).
a) Tọa độ các điểm \(E,F\) là \(E\left( { - 2\sqrt 2 ;2\sqrt 2 } \right),F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Chào mừng tháng Thanh niên. Đoàn trường THPT X tổ chức cải tạo một khoảng đất trong khuôn viên nhà trường có hình dạng là một đường tròn có đường kính \(8\,{\rm{m}}\). Để tăng tính thẩm mỹ, khi thực hiện cải tạo đã chia mảnh đất đó thành hai phần bằng một đường cong là một phần của đồ thị hàm số bậc ba \(y = f\left( x \right)\), phần gạch chéo dùng để trồng hoa và phần còn lại dùng để trồng cỏ, được mô hình hóa trong hệ trục \(Oxy\) như hình vẽ dưới đây.

Biết đồ thị hàm số bậc ba \(y = f\left( x \right)\) có tâm đối xứng trùng với gốc tọa độ; đi qua các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung và đi qua các giao điểm của đường tròn với trục \(Ox\).
a) Tọa độ các điểm \(E,F\) là \(E\left( { - 2\sqrt 2 ;2\sqrt 2 } \right),F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Quảng cáo
Trả lời:
a) Đúng. Vì các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung nên \(E = \left( { - 4\cos 45^\circ ;4\sin 45^\circ } \right) = \left( { - 2\sqrt 2 ;2\sqrt 2 } \right)\), tương tự \(F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Câu hỏi cùng đoạn
Câu 2:
b) Biết \(y = f\left( x \right) = a{x^3} + bx\). Khi đó \(a + b = - 15\).
b) Biết \(y = f\left( x \right) = a{x^3} + bx\). Khi đó \(a + b = - 15\).
b) Sai. Hàm số bậc ba có dạng \(y = f\left( x \right) = a{x^3} + c{x^2} + bx + d\left( {a \ne 0} \right)\).
Ta có \(f'\left( x \right) = 3a{x^2} + 2cx + b\); \(f''\left( x \right) = 6ax + 2c\).
Đồ thị hàm số đi qua các điểm \(C\left( { - 4;0} \right),A\left( {4;0} \right)\) và có tâm đối xứng là gốc tọa độ nên ta có:
\(\left\{ \begin{array}{l}f\left( { - 4} \right) = 0\\f\left( 4 \right) = 0\\f''\left( 0 \right) = 0\\f\left( 0 \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}64a + 4b = 0\\c = 0\\d = 0\end{array} \right. \Rightarrow b = - 16a \Rightarrow f\left( x \right) = a{x^3} - 16ax\).
Đồ thị hàm số \(f\left( x \right) = a{x^3} - 16ax\) đi qua các điểm \(E\left( { - 2\sqrt 2 ;2\sqrt 2 } \right),F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\) nên \(a = \frac{1}{8}\); \(b = - 16a = - 2\). Suy ra \(a + b = - \frac{{15}}{2}\).
Câu 3:
c) Diện tích phần trồng hoa là \(S = 16 + 8\pi \,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
c) Diện tích phần trồng hoa là \(S = 16 + 8\pi \,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
c) Đúng. Diện tích phần trồng hoa là \(S = \frac{1}{2} \cdot \pi \cdot {4^2} + 2 \cdot \int\limits_{ - 4}^0 {\left( {\frac{1}{8}{x^3} - 2x} \right)} \,{\rm{d}}x = 8\pi + 16\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Câu 4:
d) Biết chi phí trồng hoa \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(180\) nghìn đồng, trồng cỏ \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(100\) nghìn đồng. Chi phí để hoàn thành công trình trên là \(8117\) nghìn đồng (làm tròn kết quả đến hàng nghìn).
d) Biết chi phí trồng hoa \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(180\) nghìn đồng, trồng cỏ \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(100\) nghìn đồng. Chi phí để hoàn thành công trình trên là \(8117\) nghìn đồng (làm tròn kết quả đến hàng nghìn).
d) Sai. Diện tích phần trồng cỏ là \(S = \pi \cdot {4^2} - \left( {8\pi + 16} \right) = 8\pi - 16\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Chi phí để hoàn thành công trình trên là \(\left( {8\pi + 16} \right) \cdot 180 + \left( {8\pi - 16} \right) \cdot 100 \approx 8317\) (nghìn đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2,07.
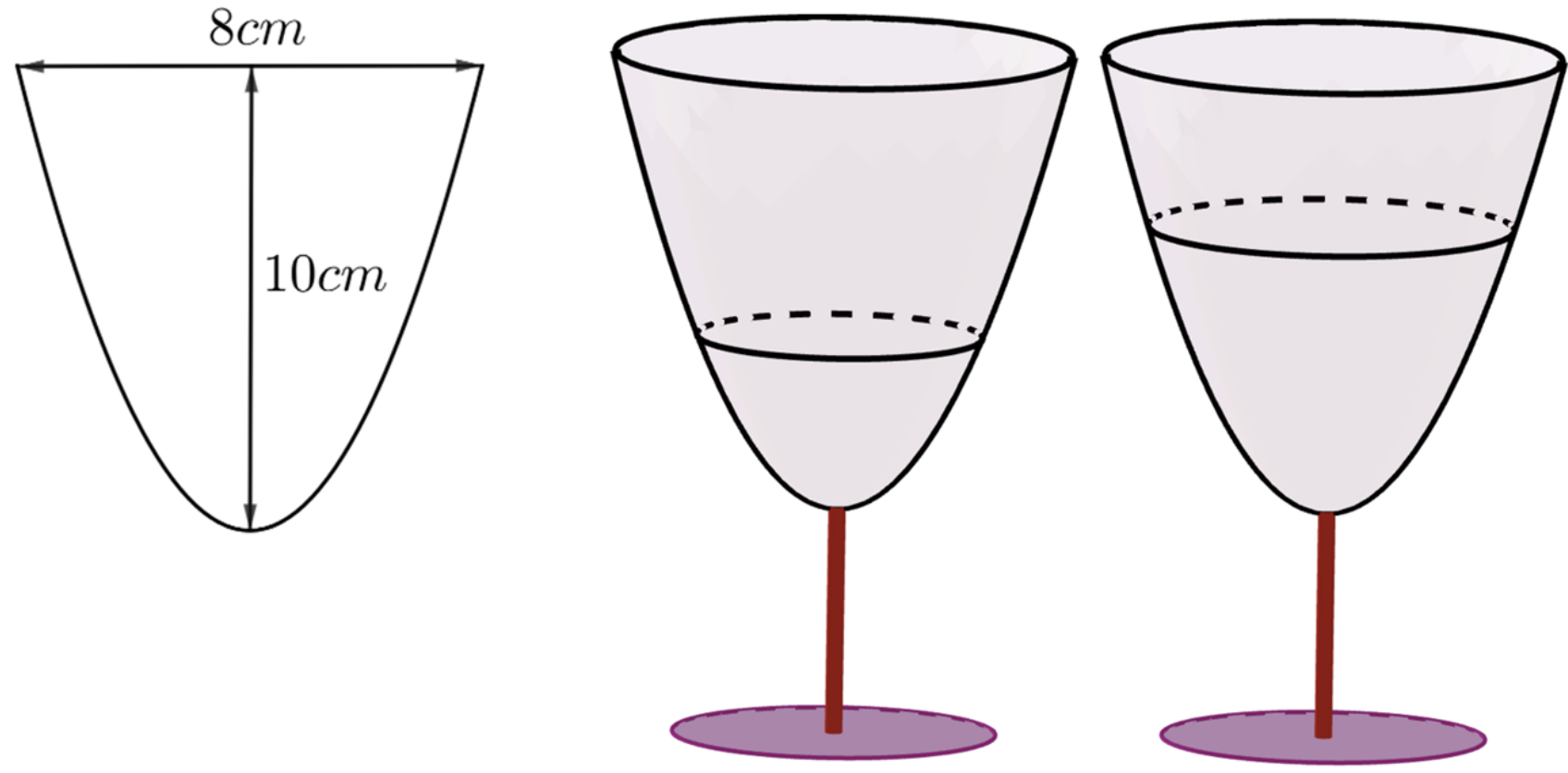
Chọn hệ trục tọa độ Oxy như hình vẽ dưới đây:
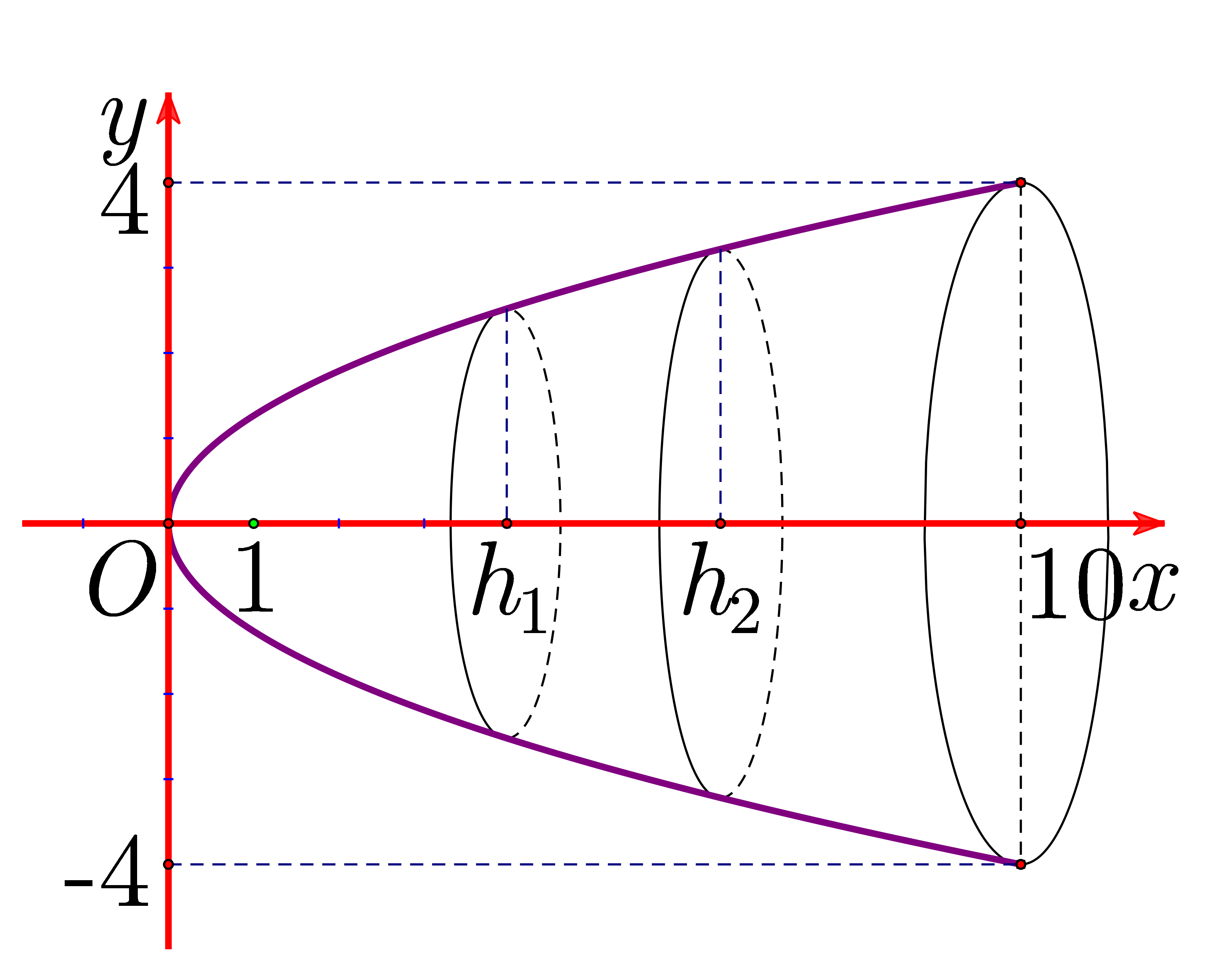
Gọi dạng của parabol là \(\left( P \right):{y^2} = 2px\).
Ta có \(x = 10,y = 4 \Rightarrow p = \frac{4}{5} \Rightarrow \left( P \right):{y^2} = \frac{8}{5}x\).
Thể tích ly nước nếu đổ đầy: \(V = \pi \int\limits_0^{10} {{y^2}{\rm{d}}x} = \pi \int\limits_0^{10} {\frac{8}{5}x{\rm{d}}x} = \left. {\frac{{4\pi {x^2}}}{5}} \right|_0^{10} = 80\pi .\)
Thể tích của nước trong ly lúc mới đổ lần đầu là: \(\pi \int\limits_0^{{h_1}} {\frac{8}{5}x{\rm{d}}x} = \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_1^2}}{5} = 20 \Rightarrow {h_1} = 5\).
Khi đó, chiều cao của nước ban đầu là \({h_1} = 5\,\left( {{\rm{cm}}} \right)\).
Thể tích của nước trong ly sau khi đổ thêm là: \(\pi \int\limits_0^{{h_2}} {\frac{8}{5}x{\rm{d}}x} = 2 \cdot \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_2^2}}{5} = 40 \Rightarrow {h_2} = 5\sqrt 2 \).
Chiều cao của mực nước sau khi đổ thêm là \({h_2} = 5\sqrt 2 \,\,\left( {{\rm{cm}}} \right)\).
Chiều cao của mực nước tăng thêm so với ban đầu: \(h = {h_2} - {h_1} = 5\sqrt 2 - 5 \approx 2,07{\rm{ (cm)}}{\rm{.}}\)
Lời giải
Đáp án: \(0,5\).
Gọi \(A\) là biến cố: “Trong 3 viên bi lấy ra từ hộp hai có 2 viên bi từ hộp thứ nhất chuyển sang”.
Gọi \(B\) là biến cố: “Ba viên bi lấy ra từ hộp hai là màu trắng”.
Trường hợp 1: 2 viên bi từ hộp thứ nhất chuyển sang là 2 viên bi trắng. Khi đó:
\({P_1}\left( B \right) = \frac{{C_7^2}}{{C_{12}^2}} \cdot \frac{{C_6^3}}{{C_{12}^3}} = \frac{7}{{242}}\).
Trường hợp 2: 2 viên bi từ hộp thứ nhất chuyển sang là 2 viên bi đỏ. Khi đó:
\({P_2}\left( B \right) = \frac{{C_5^2}}{{C_{12}^2}} \cdot \frac{{C_4^3}}{{C_{12}^3}} = \frac{1}{{363}}\).
Trường hợp 3: 2 viên bi từ hộp thứ nhất chuyển sang là 1 viên bi trắng và 1 viên bi đỏ. Khi đó:
\({P_3}\left( B \right) = \frac{{C_7^1.C_5^1}}{{C_{12}^2}} \cdot \frac{{C_5^3}}{{C_{12}^3}} = \frac{{35}}{{1452}}\).
Suy ra \(P\left( B \right) = {P_1}\left( B \right) + {P_2}\left( B \right) + {P_3}\left( B \right) = \frac{{27}}{{284}}\) và \(P\left( {AB} \right) = {P_1}\left( B \right) = \frac{7}{{242}}\).
Do đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{\frac{7}{{242}}}}{{\frac{{27}}{{484}}}} = \frac{{14}}{{27}} \approx 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.