Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(3\) và cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Biết góc nhị diện \(\left[ {B,SC,D} \right]\) bằng \(120^\circ \). Tính thể tích khối chóp \(S.ABCD\) bằng bao nhiêu?
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(3\) và cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Biết góc nhị diện \(\left[ {B,SC,D} \right]\) bằng \(120^\circ \). Tính thể tích khối chóp \(S.ABCD\) bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(9\).
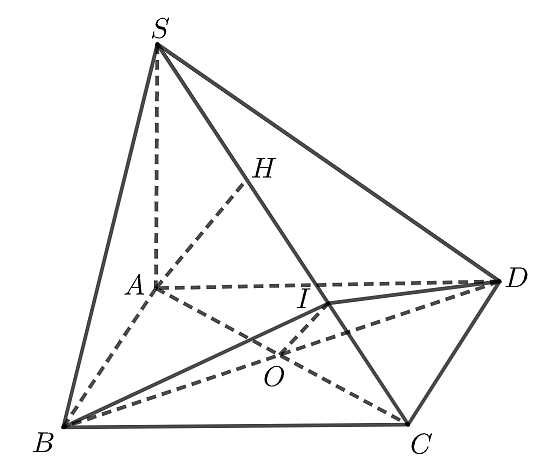
Gọi \(O\) là tâm của hình vuông \(ABCD\).
Trong mặt phẳng \(\left( {SAC} \right)\) kẻ \(OI \bot SC\) tại \(I\); \(AH \bot SC\) tại \(H\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{BD \bot SA}\\{BD \bot AC}\end{array} \Rightarrow BD \bot \left( {SAC} \right)} \right.\), \(OI \subset \left( {SAC} \right) \Rightarrow OI \bot BD\) và \(BD \bot SC\).
Vậy \(SC \bot \left( {BID} \right) \Rightarrow SC \bot BI;\,SC \bot DI\) nên góc phẳng nhị diện \(\left[ {B,SC,D} \right]\) bằng \(\widehat {BID}\).
\( \Rightarrow \widehat {BID} = 120^\circ \). Suy ra \(\widehat {BIO} = 60^\circ \).
Khi đó, \(\tan \widehat {BIO} = \frac{{BO}}{{OI}} \Rightarrow \tan 60^\circ = \frac{{\frac{{\sqrt 2 }}{2} \cdot 3}}{{OI}} \Leftrightarrow OI = \frac{{\sqrt 6 }}{2} \Rightarrow AH = \sqrt 6 \).
Tam giác vuông \(SAC\) có đường cao \(AH \Rightarrow \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}} \Rightarrow SA = 3.\)
Vậy thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}SA \cdot {S_{ABCD}} = \frac{1}{3} \cdot 3 \cdot 9 = 9\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2,07.
Chọn hệ trục tọa độ Oxy như hình vẽ dưới đây:
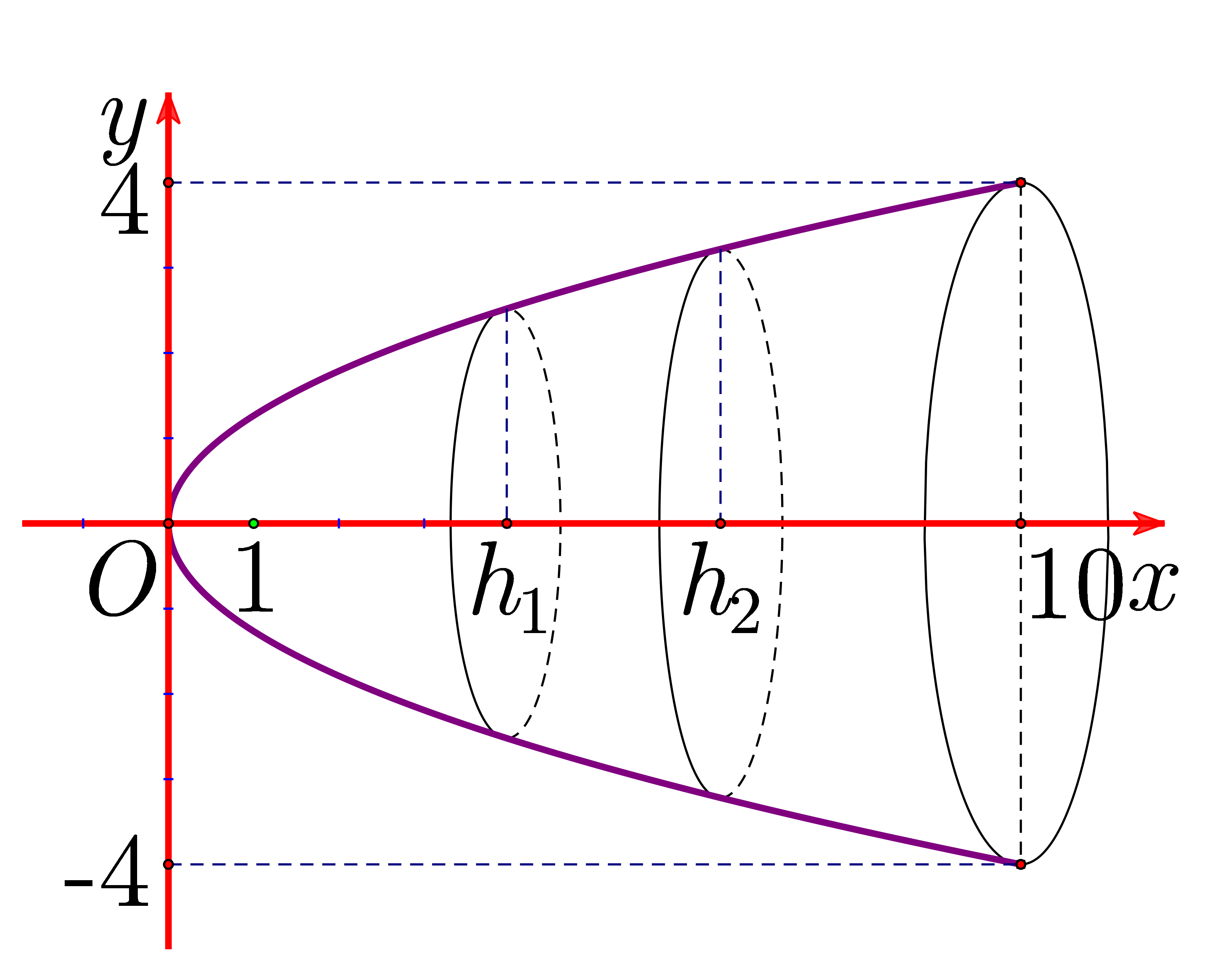
Gọi dạng của parabol là \(\left( P \right):{y^2} = 2px\).
Ta có \(x = 10,y = 4 \Rightarrow p = \frac{4}{5} \Rightarrow \left( P \right):{y^2} = \frac{8}{5}x\).
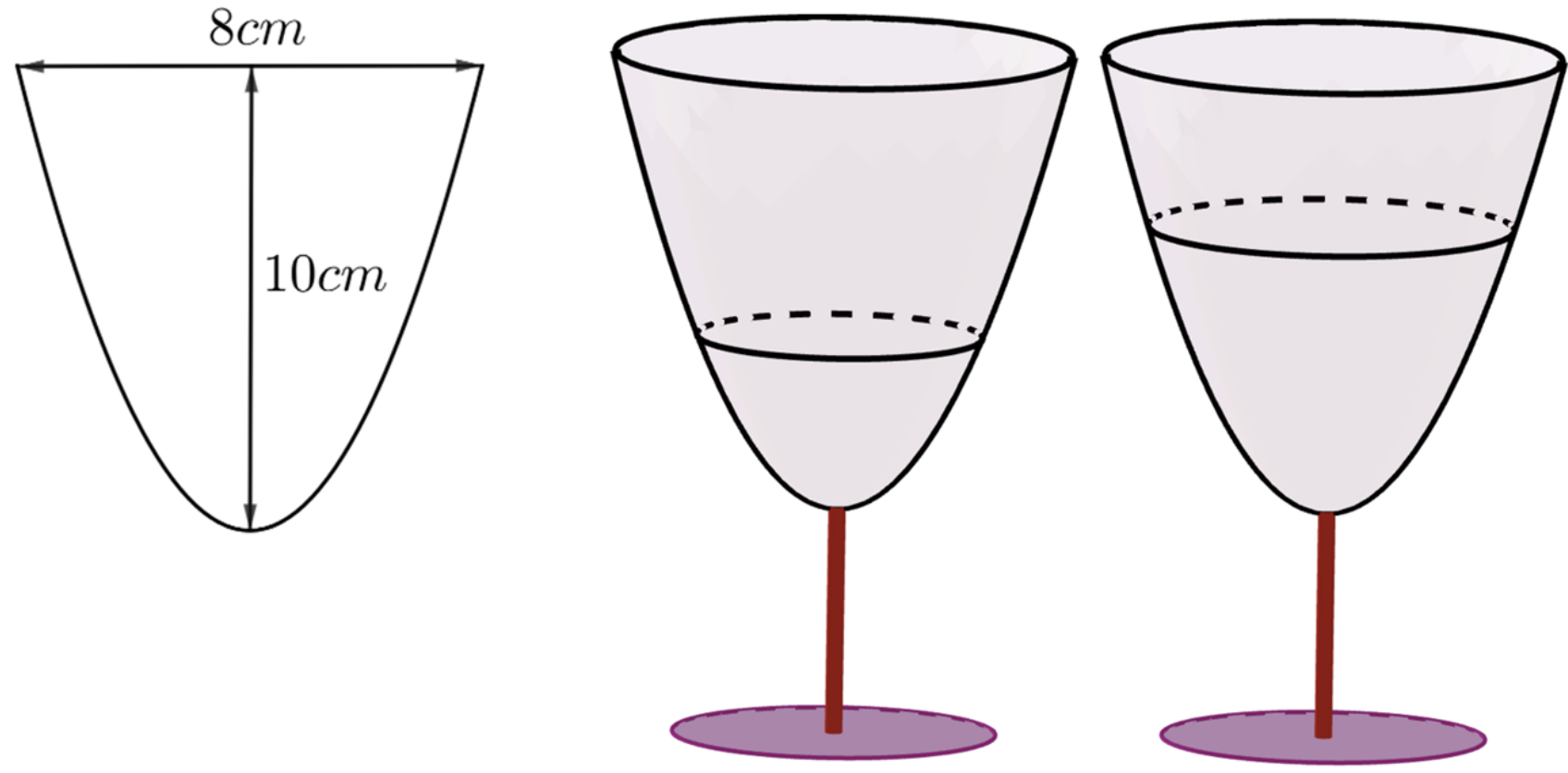
Thể tích ly nước nếu đổ đầy: \(V = \pi \int\limits_0^{10} {{y^2}{\rm{d}}x} = \pi \int\limits_0^{10} {\frac{8}{5}x{\rm{d}}x} = \left. {\frac{{4\pi {x^2}}}{5}} \right|_0^{10} = 80\pi .\)
Thể tích của nước trong ly lúc mới đổ lần đầu là: \(\pi \int\limits_0^{{h_1}} {\frac{8}{5}x{\rm{d}}x} = \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_1^2}}{5} = 20 \Rightarrow {h_1} = 5\).
Khi đó, chiều cao của nước ban đầu là \({h_1} = 5\,\left( {{\rm{cm}}} \right)\).
Thể tích của nước trong ly sau khi đổ thêm là: \(\pi \int\limits_0^{{h_2}} {\frac{8}{5}x{\rm{d}}x} = 2 \cdot \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_2^2}}{5} = 40 \Rightarrow {h_2} = 5\sqrt 2 \).
Chiều cao của mực nước sau khi đổ thêm là \({h_2} = 5\sqrt 2 \,\,\left( {{\rm{cm}}} \right)\).
Chiều cao của mực nước tăng thêm so với ban đầu: \(h = {h_2} - {h_1} = 5\sqrt 2 - 5 \approx 2,07{\rm{ (cm)}}{\rm{.}}\)
Lời giải
a) Đúng. Vì các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung nên \(E = \left( { - 4\cos 45^\circ ;4\sin 45^\circ } \right) = \left( { - 2\sqrt 2 ;2\sqrt 2 } \right)\), tương tự \(F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập