Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí \(A\) cao \(15{\rm{\;m}}\) của tháp 1 này sang vị trí \(B\) cao \(10{\rm{\;m}}\) của tháp 2 trong khung cảnh tuyệt đẹp xung quanh.
Với hệ trục toạ độ \(Oxyz\) cho trước (đơn vị: mét), toạ độ của \(A\) và \(B\) lần lượt là \(A\left( {3;2,5;15} \right)\) và \(B\left( {21;27,5;10} \right)\). Khi du khách khi ở độ cao 12 mét thì tọa độ của du khách lúc đó là \(M\left( {a;b;c} \right)\). Tính giá trị biểu thức \(T = a + b + c\).
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí \(A\) cao \(15{\rm{\;m}}\) của tháp 1 này sang vị trí \(B\) cao \(10{\rm{\;m}}\) của tháp 2 trong khung cảnh tuyệt đẹp xung quanh.
Với hệ trục toạ độ \(Oxyz\) cho trước (đơn vị: mét), toạ độ của \(A\) và \(B\) lần lượt là \(A\left( {3;2,5;15} \right)\) và \(B\left( {21;27,5;10} \right)\). Khi du khách khi ở độ cao 12 mét thì tọa độ của du khách lúc đó là \(M\left( {a;b;c} \right)\). Tính giá trị biểu thức \(T = a + b + c\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(43,3\).
Phương trình đường thẳng chứa đường trượt zipline là đường thẳng\(AB\).
Ta có \(A\left( {3;2,5;15} \right)\), \(B\left( {21;27,5;10} \right) \Rightarrow \overrightarrow {AB} = \left( {18;25; - 5} \right)\).
Phương trình đường thẳng chứa đường trượt zipline là \(\left\{ \begin{array}{l}x = 3 + 18t\\y = 2,5 + 25t\\z = 15 - 5t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).
Khi du khách khi ở độ cao 12 mét \( \Rightarrow z = 12 \Rightarrow 15 - 5t = 12 \Rightarrow t = \frac{3}{5}\).
Thay \(t = \frac{3}{5}\) vào phương trình đường thẳng \(AB\) ta được \(\left\{ \begin{array}{l}x = 13,8\\y = 17,5\\z = 12\end{array} \right.{\rm{ }} \Rightarrow M\left( {13,8;17,5;12} \right)\).
Vậy \(T = a + b + c = 13,8 + 17,5 + 12 = 43,3.\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2,07.
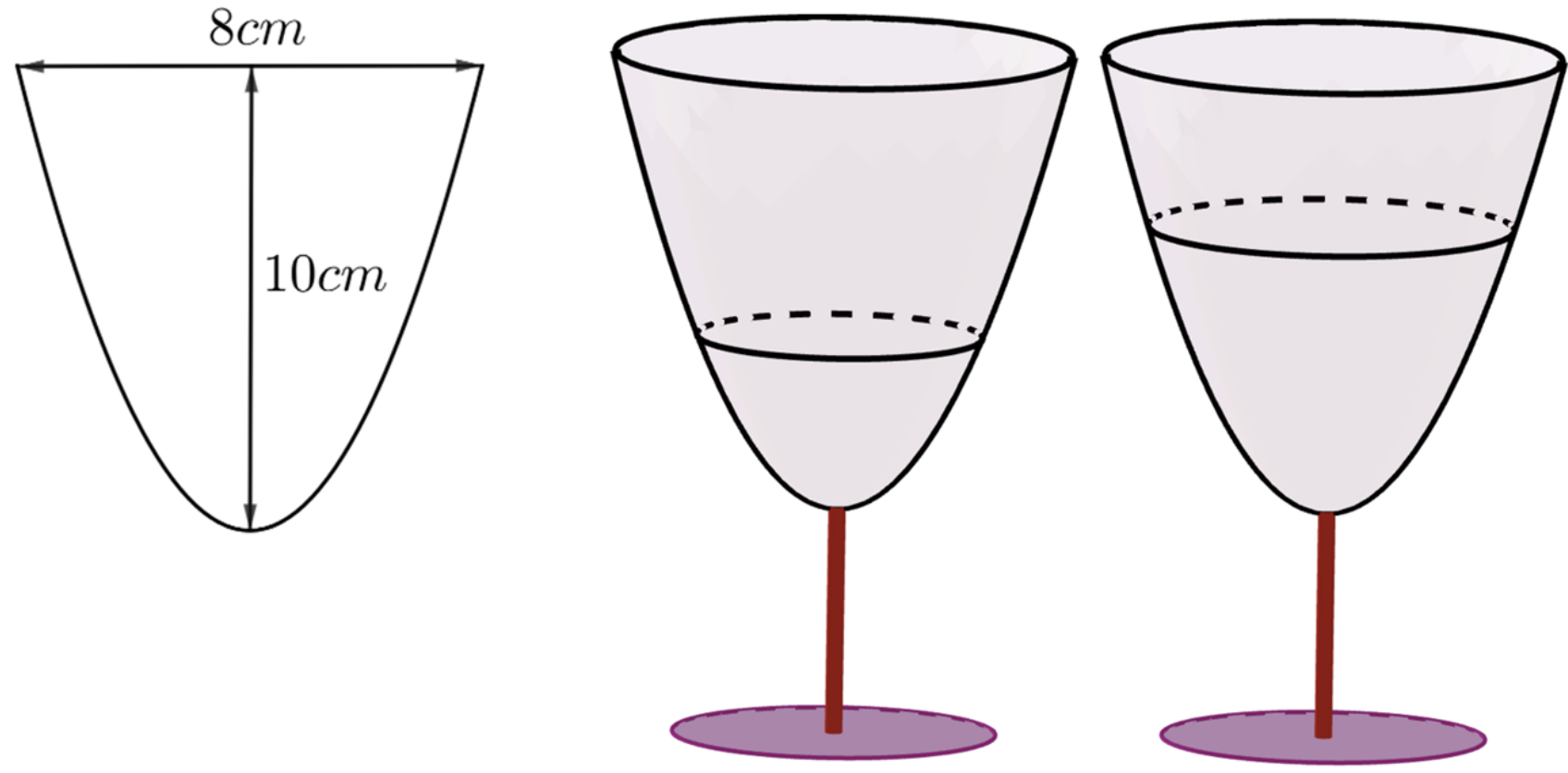
Chọn hệ trục tọa độ Oxy như hình vẽ dưới đây:
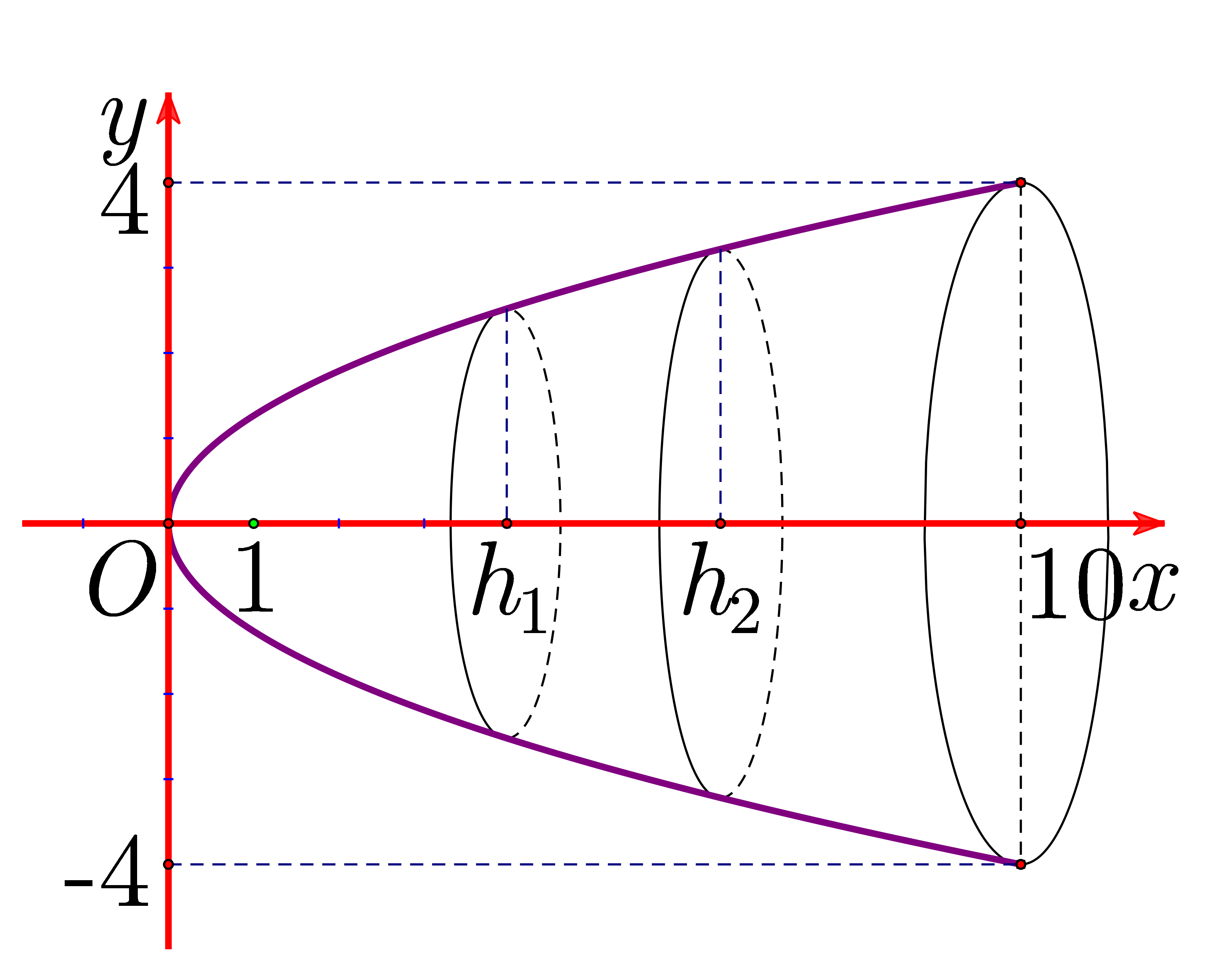
Gọi dạng của parabol là \(\left( P \right):{y^2} = 2px\).
Ta có \(x = 10,y = 4 \Rightarrow p = \frac{4}{5} \Rightarrow \left( P \right):{y^2} = \frac{8}{5}x\).
Thể tích ly nước nếu đổ đầy: \(V = \pi \int\limits_0^{10} {{y^2}{\rm{d}}x} = \pi \int\limits_0^{10} {\frac{8}{5}x{\rm{d}}x} = \left. {\frac{{4\pi {x^2}}}{5}} \right|_0^{10} = 80\pi .\)
Thể tích của nước trong ly lúc mới đổ lần đầu là: \(\pi \int\limits_0^{{h_1}} {\frac{8}{5}x{\rm{d}}x} = \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_1^2}}{5} = 20 \Rightarrow {h_1} = 5\).
Khi đó, chiều cao của nước ban đầu là \({h_1} = 5\,\left( {{\rm{cm}}} \right)\).
Thể tích của nước trong ly sau khi đổ thêm là: \(\pi \int\limits_0^{{h_2}} {\frac{8}{5}x{\rm{d}}x} = 2 \cdot \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_2^2}}{5} = 40 \Rightarrow {h_2} = 5\sqrt 2 \).
Chiều cao của mực nước sau khi đổ thêm là \({h_2} = 5\sqrt 2 \,\,\left( {{\rm{cm}}} \right)\).
Chiều cao của mực nước tăng thêm so với ban đầu: \(h = {h_2} - {h_1} = 5\sqrt 2 - 5 \approx 2,07{\rm{ (cm)}}{\rm{.}}\)
Lời giải
a) Đúng. Vì các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung nên \(E = \left( { - 4\cos 45^\circ ;4\sin 45^\circ } \right) = \left( { - 2\sqrt 2 ;2\sqrt 2 } \right)\), tương tự \(F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập