Để tạo một kiện hàng dạng hình lăng trụ đứng với đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng, người ta dùng các thanh gỗ ghép khít đóng lại với nhau. Biết rằng, dung tích kiện hàng bằng \(9\,{{\rm{m}}^{\rm{3}}}\) và giá thành \(1\,{{\rm{m}}^{\rm{2}}}\) gỗ sử dụng là \(200\,000\) đồng.

Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).

Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).
Quảng cáo
Trả lời:
Gọi \(x\,\,\left( {{\rm{m}},\,x > 0} \right)\) là chiều rộng của đáy kiện hàng. Khi đó chiều dài của kiện hàng là \(2x\,\left( {\rm{m}} \right)\) và chiều cao của kiện hàng là \(\frac{9}{{2{x^2}}}\,\left( {\rm{m}} \right)\). Khi đó diện tích của kiện hàng là \(4{x^2} + \frac{{27}}{x}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Xét hàm số \(f\left( x \right) = 4{x^2} + \frac{{27}}{x}\) có \(f'\left( x \right) = 8x - \frac{{27}}{{{x^2}}} = 0 \Leftrightarrow x = 1,5\).
Bảng biến thiên của hàm số \(f\left( x \right)\) như sau:
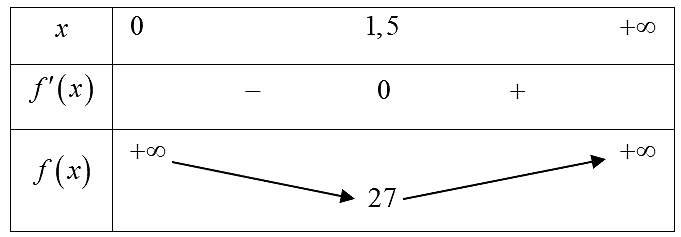
Từ bảng biên thiên ta có \(\min \,f\left( x \right) = f\left( {1,5} \right) = 27\).
Vậy chi phí thấp nhất làm kiện hàng là: \(200\,000 \cdot 27 = 5\,400\,000\) đồng \( = 5,4\) triệu đồng.
Đáp án: \(5,4\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\left( { - \infty ;0} \right)\).
Lời giải
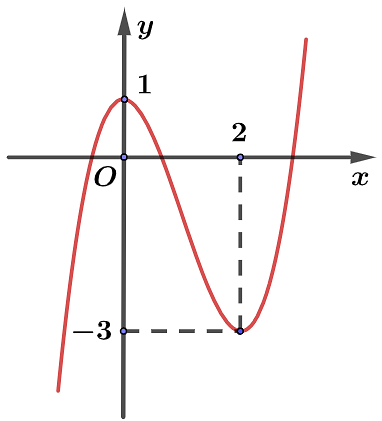
Từ đồ thị, ta thấy hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\). Chọn D.
Câu 2
Lời giải
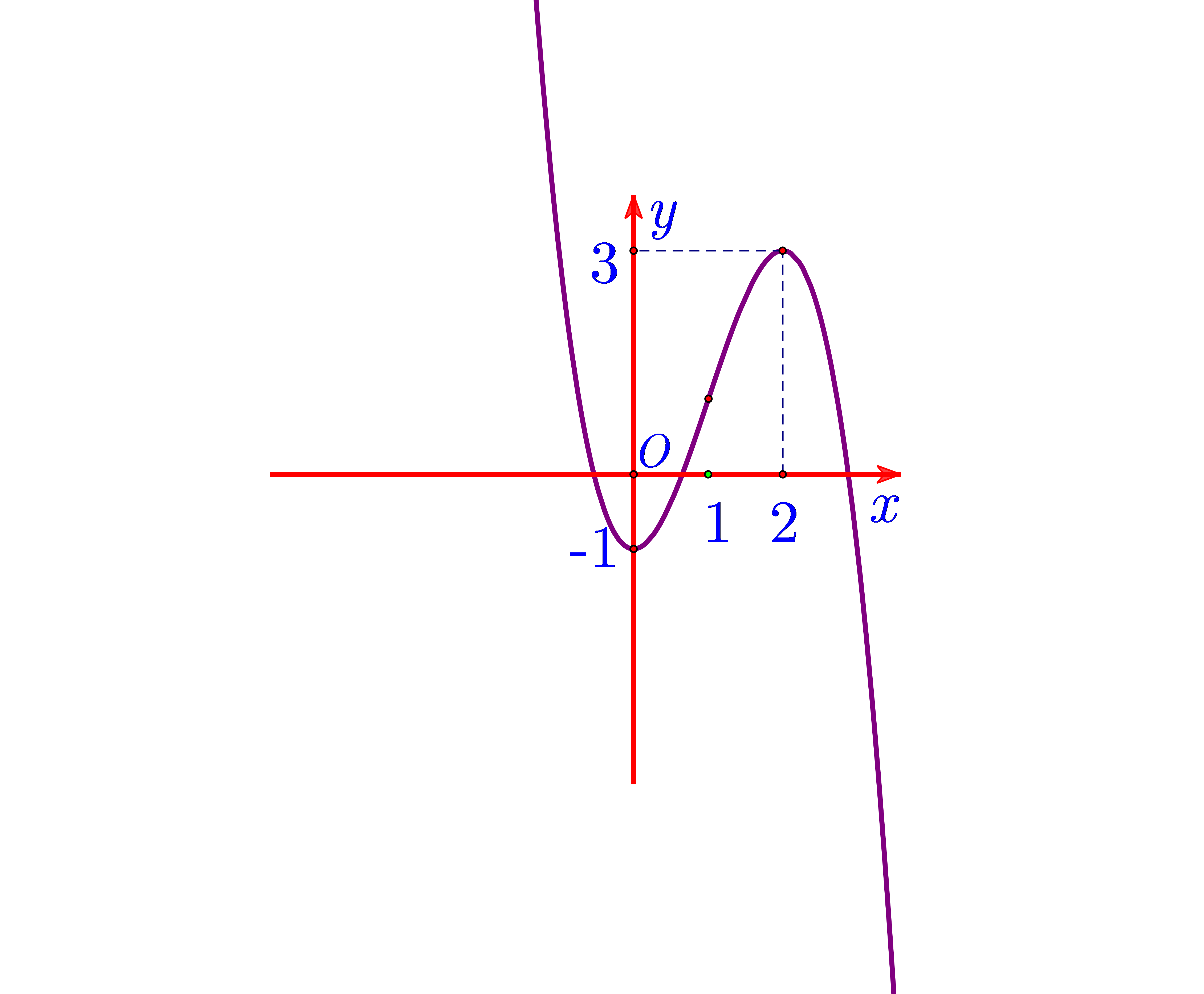
Vì \(f'\left( x \right) = 0\) có 3 nghiệm lẻ nên hàm số \(y = f\left( x \right)\) có 3 cực trị. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.