PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
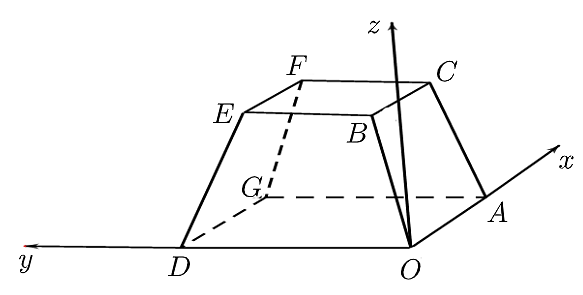
Một sân vận động được xây dựng theo mô hình là hình chóp cụt \(OAGD.BCFE\) có hai đáy song song với nhau. Mặt sân \(OAGD\) là hình chữ nhật và được gắn hệ trục \[Oxyz\] như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân \(OAGD\) có chiều dài \(OA = 100\,\,{\rm{m}}\), chiều rộng \(OD = 60\,\,{\rm{m}}\) và tọa độ điểm \(B\left( {10;10;8} \right)\).
a) \(\overrightarrow {OD} = \left( {0;60;0} \right)\).
b) \(G\left( {100;\,\,0;\,\,60} \right)\).
c) Phương trình mặt phẳng \(\left( {OBED} \right)\) là: \(4x - 5z = 0\).
d) Khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {OBED} \right)\) (kết quả làm tròn đến chữ số thập phân thứ nhất) là \(62,4\,\,{\rm{m}}\).
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một sân vận động được xây dựng theo mô hình là hình chóp cụt \(OAGD.BCFE\) có hai đáy song song với nhau. Mặt sân \(OAGD\) là hình chữ nhật và được gắn hệ trục \[Oxyz\] như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân \(OAGD\) có chiều dài \(OA = 100\,\,{\rm{m}}\), chiều rộng \(OD = 60\,\,{\rm{m}}\) và tọa độ điểm \(B\left( {10;10;8} \right)\).

a) \(\overrightarrow {OD} = \left( {0;60;0} \right)\).
b) \(G\left( {100;\,\,0;\,\,60} \right)\).
c) Phương trình mặt phẳng \(\left( {OBED} \right)\) là: \(4x - 5z = 0\).
d) Khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {OBED} \right)\) (kết quả làm tròn đến chữ số thập phân thứ nhất) là \(62,4\,\,{\rm{m}}\).
Quảng cáo
Trả lời:
Ta có \(OD = 60\,\,{\rm{m}}\) và \(D \in Oy\) nên \(D\left( {0;60;0} \right)\). Suy ra \(\overrightarrow {OD} = \left( {0;60;0} \right)\).
Có \(OA = 100\,\,{\rm{m}}\) và \(A \in Ox\) nên \(A\left( {100\,;\,0\,;\,0} \right)\). Suy ra \(\overrightarrow {OA} = \left( {100\,;\,0\,;\,0} \right)\).
Vì \(OAGD\) là hình chữ nhật nên \(\overrightarrow {OG} = \overrightarrow {OD} + \overrightarrow {OA} = \left( {100;60;0} \right)\). Do đó, \(G\left( {100;\,\,60;\,\,0} \right)\).
Ta có \(B\left( {10;10;8} \right)\) nên \(\overrightarrow {OB} = \left( {10;10;8} \right)\).
Xét \(\vec n = \left[ {\overrightarrow {OD} ,\overrightarrow {OB} } \right] = \left( {480;0; - 600} \right) = 120\left( {4;0; - 5} \right)\). Khi đó, \(\vec n' = \left( {4\,;\,0\,;\, - 5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OBED} \right)\).
Mặt phẳng \(\left( {OBED} \right)\) đi qua \[O\left( {0;0;0} \right)\] và có vectơ pháp tuyến \(\vec n' = \left( {4\,;\,0\,;\, - 5} \right)\) nên có phương trình là: \(4x - 5z = 0\).
Khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {OBED} \right)\) là:
\(d\left( {G,\left( {OBED} \right)} \right) = \frac{{\left| {4 \cdot 100 - 5 \cdot 0} \right|}}{{\sqrt {16 + 25} }} = \frac{{400\sqrt {41} }}{{41}} \approx 62,5\,\,{\rm{m}}\).
Đáp án: a) Đúng, b) Sai, c) Đúng, d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
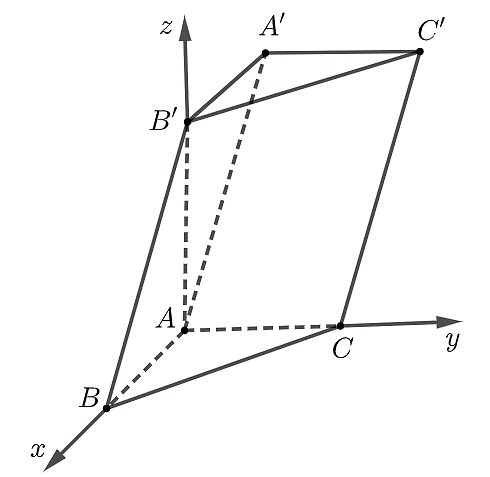
a) Tính được \[\overrightarrow {AB} = \left( {2;0;0} \right),\overrightarrow {AC} = \left( {0;3;0} \right),\overrightarrow {AB'} = \left( {0;0;4} \right) \Rightarrow AB = 2;AC = 3;AB' = 4\].
Có \[Oz \bot \left( {Oxy} \right)\] và \[AB' \subset Oz\], \[\left( {ABC} \right) \equiv \left( {Oxy} \right)\] nên \[AB' \bot \left( {ABC} \right)\].
Thể tích khối lăng trụ \[ABC.A'B'C'\] là:
\[V = d\left( {B',\left( {ABC} \right)} \right) \cdot {S_{\Delta ABC}} = AB' \cdot \frac{1}{2} \cdot AB \cdot AC = 4 \cdot \frac{1}{2} \cdot 2 \cdot 3 = 12\].
b) Gọi \[A'\left( {x;y;z} \right) \Rightarrow \overrightarrow {AA'} = \left( {x;y;z} \right)\].
Có \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], mà \[\overrightarrow {BB'} = \overrightarrow {AA'} \], suy ra toạ độ điểm \[A'\] là \[\left( { - 2;0;4} \right)\].
Từ đó ta có \[\overrightarrow {A'B} = \left( {4;0; - 4} \right),\overrightarrow {A'C} = \left( {2;3; - 4} \right)\]. Vậy \[\overrightarrow u = \overrightarrow {A'B} + \overrightarrow {A'C} \] thì \[\overrightarrow u = \left( {6;3; - 8} \right)\].
c) Gọi \[C'\left( {a;b;c} \right) \Rightarrow \overrightarrow {CC'} = \left( {a;b - 3;c} \right)\].
Ta có \[\overrightarrow {BB'} = \overrightarrow {CC'} \], mà \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], suy ra toạ độ điểm \[C'\] là \[\left( { - 2;3;4} \right)\].
d) Hình chiếu vuông góc của điểm \[B\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[A\] (do \[Ox \bot \left( {Oyz} \right)\]).
Do \[Ox\,{\rm{//}}\,A'B'\] mà \[Ox \bot \left( {Oyz} \right)\] nên \[A'B' \bot \left( {Oyz} \right)\], từ đó suy ra hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[B'\].
Gọi \[{C_1}\left( {m;n;p} \right)\] là hình chiếu vuông góc của \[C'\] lên mặt phẳng \[\left( {Oyz} \right)\]\[ \Rightarrow {C_1}\left( {0;3;4} \right)\].
Vậy hình chiếu của hình lăng trụ \[ABC.A'B'C'\] lên mặt phẳng \[\left( {Oyz} \right)\]là hình chữ nhật \[AB'{C_1}C\].
Diện tích đa giác là: \[{S_{AB'{C_1}C}} = AB' \cdot AC = 4 \cdot 3 = 12\].
Đáp án: a) Sai, b) Đúng, c) Đúng, d) Sai.
Câu 2
Lời giải
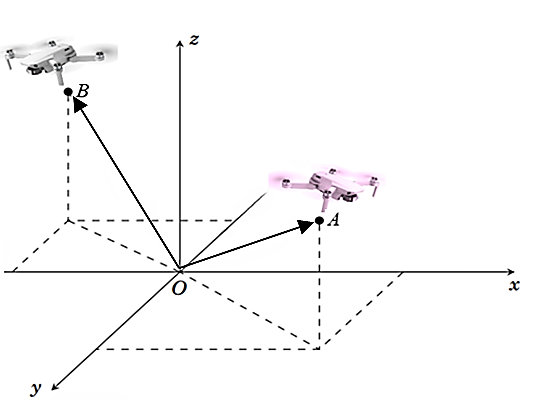
Ta có \[\vec u = 2\vec a - 3\vec b + \vec c = \left( {5\,;\,3\,;\, - 9} \right)\]. Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.