PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Trong không gian với hệ trục tọa độ \[Oxyz\], cho các điểm \[A\left( {1;0;0} \right)\], \[B\left( {0;b;0} \right)\], \[C\left( {0;0;c} \right)\] trong đó \[b,c\] là các số hữu tỷ dương và mặt phẳng \[\left( P \right)\] có phương trình \[y - z + 1 = 0\]. Biết rằng mặt phẳng \[\left( {ABC} \right)\] vuông góc với mặt phẳng \[\left( P \right)\] và khoảng cách từ \[O\] đến mặt phẳng \[\left( {ABC} \right)\] bằng \[\frac{1}{3}\]. Tính \[b + c\].
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Trong không gian với hệ trục tọa độ \[Oxyz\], cho các điểm \[A\left( {1;0;0} \right)\], \[B\left( {0;b;0} \right)\], \[C\left( {0;0;c} \right)\] trong đó \[b,c\] là các số hữu tỷ dương và mặt phẳng \[\left( P \right)\] có phương trình \[y - z + 1 = 0\]. Biết rằng mặt phẳng \[\left( {ABC} \right)\] vuông góc với mặt phẳng \[\left( P \right)\] và khoảng cách từ \[O\] đến mặt phẳng \[\left( {ABC} \right)\] bằng \[\frac{1}{3}\]. Tính \[b + c\].
Quảng cáo
Trả lời:
Ta có phương trình mặt phẳng \[\left( {ABC} \right)\]: \[\frac{x}{1} + \frac{y}{b} + \frac{z}{c} = 1 \Leftrightarrow \frac{x}{1} + \frac{y}{b} + \frac{z}{c} - 1 = 0\].
Suy ra một vectơ pháp tuyến của mặt phẳng \[\left( {ABC} \right)\] là \[{\vec n_{\left( {ABC} \right)}} = \left( {1;\frac{1}{b};\frac{1}{c}} \right)\].
Vectơ pháp tuyến của mặt phẳng \[\left( P \right)\] là \[{\vec n_{\left( P \right)}} = \left( {0;1; - 1} \right)\].
Theo giả thiết: \[\left( {ABC} \right) \bot \left( P \right)\] nên \[{\vec n_{\left( {ABC} \right)}} \cdot {\vec n_{\left( P \right)}} = 0\] hay \[\frac{1}{b} - \frac{1}{c} = 0\,\, \Leftrightarrow \,\,b = c\,\,\left( 1 \right)\].
Mà \[d\left( {O,\left( {ABC} \right)} \right) = \frac{{\left| { - 1} \right|}}{{\sqrt {1 + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }} = \frac{1}{3}\] hay \[\sqrt {1 + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} = 3\,\, \Leftrightarrow \,\,1 + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = 9\,\,\left( 2 \right)\].
Thay \[\left( 1 \right)\] vào \[\left( 2 \right)\] ta được: \[1 + \frac{1}{{{b^2}}} + \frac{1}{{{b^2}}} = 9\, \Leftrightarrow \frac{2}{{{b^2}}} = 8 \Leftrightarrow {b^2} = \frac{1}{4} \Rightarrow b = \frac{1}{2}\] (vì \[b\]là số hữu tỷ dương).
Suy ra \[c = \frac{1}{2}\]. Vậy \[b + c = 1\].
Đáp án: \(1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
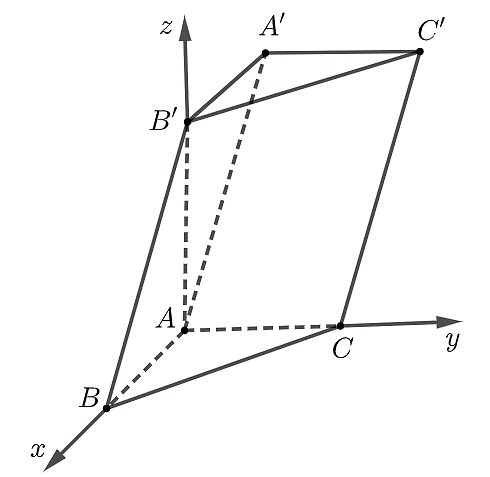
a) Tính được \[\overrightarrow {AB} = \left( {2;0;0} \right),\overrightarrow {AC} = \left( {0;3;0} \right),\overrightarrow {AB'} = \left( {0;0;4} \right) \Rightarrow AB = 2;AC = 3;AB' = 4\].
Có \[Oz \bot \left( {Oxy} \right)\] và \[AB' \subset Oz\], \[\left( {ABC} \right) \equiv \left( {Oxy} \right)\] nên \[AB' \bot \left( {ABC} \right)\].
Thể tích khối lăng trụ \[ABC.A'B'C'\] là:
\[V = d\left( {B',\left( {ABC} \right)} \right) \cdot {S_{\Delta ABC}} = AB' \cdot \frac{1}{2} \cdot AB \cdot AC = 4 \cdot \frac{1}{2} \cdot 2 \cdot 3 = 12\].
b) Gọi \[A'\left( {x;y;z} \right) \Rightarrow \overrightarrow {AA'} = \left( {x;y;z} \right)\].
Có \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], mà \[\overrightarrow {BB'} = \overrightarrow {AA'} \], suy ra toạ độ điểm \[A'\] là \[\left( { - 2;0;4} \right)\].
Từ đó ta có \[\overrightarrow {A'B} = \left( {4;0; - 4} \right),\overrightarrow {A'C} = \left( {2;3; - 4} \right)\]. Vậy \[\overrightarrow u = \overrightarrow {A'B} + \overrightarrow {A'C} \] thì \[\overrightarrow u = \left( {6;3; - 8} \right)\].
c) Gọi \[C'\left( {a;b;c} \right) \Rightarrow \overrightarrow {CC'} = \left( {a;b - 3;c} \right)\].
Ta có \[\overrightarrow {BB'} = \overrightarrow {CC'} \], mà \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], suy ra toạ độ điểm \[C'\] là \[\left( { - 2;3;4} \right)\].
d) Hình chiếu vuông góc của điểm \[B\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[A\] (do \[Ox \bot \left( {Oyz} \right)\]).
Do \[Ox\,{\rm{//}}\,A'B'\] mà \[Ox \bot \left( {Oyz} \right)\] nên \[A'B' \bot \left( {Oyz} \right)\], từ đó suy ra hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[B'\].
Gọi \[{C_1}\left( {m;n;p} \right)\] là hình chiếu vuông góc của \[C'\] lên mặt phẳng \[\left( {Oyz} \right)\]\[ \Rightarrow {C_1}\left( {0;3;4} \right)\].
Vậy hình chiếu của hình lăng trụ \[ABC.A'B'C'\] lên mặt phẳng \[\left( {Oyz} \right)\]là hình chữ nhật \[AB'{C_1}C\].
Diện tích đa giác là: \[{S_{AB'{C_1}C}} = AB' \cdot AC = 4 \cdot 3 = 12\].
Đáp án: a) Sai, b) Đúng, c) Đúng, d) Sai.
Câu 2
Lời giải
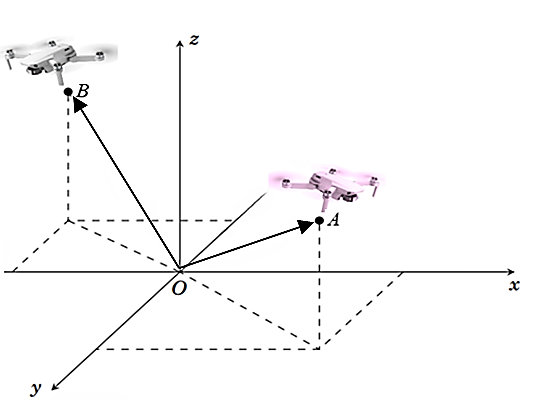
Ta có \[\vec u = 2\vec a - 3\vec b + \vec c = \left( {5\,;\,3\,;\, - 9} \right)\]. Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.