Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam \(2\,{\rm{m}}\), cách bạn nữ \(4\,{\rm{m}}\). Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Biết rằng phương trình của \(\left( P \right)\) trong không gian \[Oxyz\] được mô tả như trong hình vẽ và có dạng \(\left( P \right):ax + by + cz = 0\). Khi đó giá trị của \({a^2} - {b^2} + {c^2}\) bằng bao nhiêu?
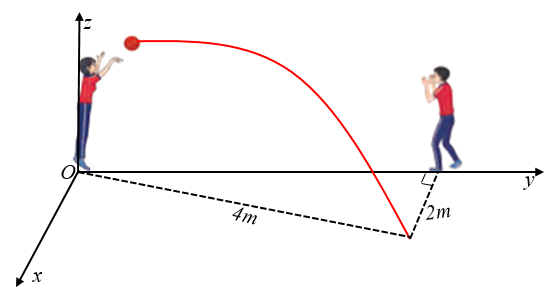
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam \(2\,{\rm{m}}\), cách bạn nữ \(4\,{\rm{m}}\). Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Biết rằng phương trình của \(\left( P \right)\) trong không gian \[Oxyz\] được mô tả như trong hình vẽ và có dạng \(\left( P \right):ax + by + cz = 0\). Khi đó giá trị của \({a^2} - {b^2} + {c^2}\) bằng bao nhiêu?

Quảng cáo
Trả lời:
Khoảng cách giữa hai bạn học sinh là \(\sqrt {{4^2} - {2^2}} = 2\sqrt 3 \).
Gọi \(M\) là điểm mà quả bóng rơi trên mặt đất. Khi đó \(M\left( {2;2\sqrt 3 ;0} \right)\).
Mặt phẳng \(\left( P \right)\) có cặp vectơ chỉ phương là \(\vec k = \left( {0;0;1} \right)\) và \(\overrightarrow {OM} = \left( {2;2\sqrt 3 ;0} \right)\) nên mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow n = \left( { - 2\sqrt 3 ;2;0} \right)\) nên phương trình mặt phẳng \(\left( P \right): - 2\sqrt 3 x + 2y = 0\).
Vậy \({a^2} - {b^2} + {c^2} = {\left( { - 2\sqrt 3 } \right)^2} - {2^2} + {0^2} = 8\).
Đáp án: \(8\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
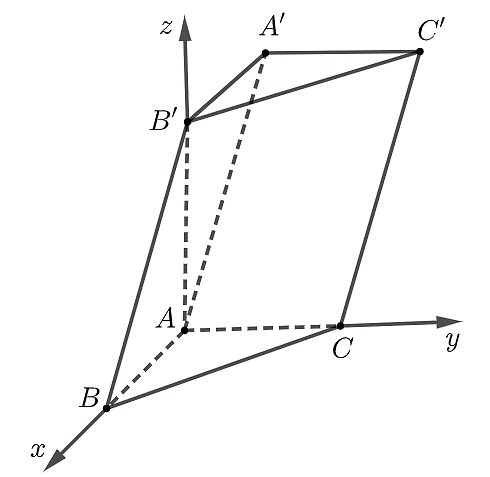
a) Tính được \[\overrightarrow {AB} = \left( {2;0;0} \right),\overrightarrow {AC} = \left( {0;3;0} \right),\overrightarrow {AB'} = \left( {0;0;4} \right) \Rightarrow AB = 2;AC = 3;AB' = 4\].
Có \[Oz \bot \left( {Oxy} \right)\] và \[AB' \subset Oz\], \[\left( {ABC} \right) \equiv \left( {Oxy} \right)\] nên \[AB' \bot \left( {ABC} \right)\].
Thể tích khối lăng trụ \[ABC.A'B'C'\] là:
\[V = d\left( {B',\left( {ABC} \right)} \right) \cdot {S_{\Delta ABC}} = AB' \cdot \frac{1}{2} \cdot AB \cdot AC = 4 \cdot \frac{1}{2} \cdot 2 \cdot 3 = 12\].
b) Gọi \[A'\left( {x;y;z} \right) \Rightarrow \overrightarrow {AA'} = \left( {x;y;z} \right)\].
Có \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], mà \[\overrightarrow {BB'} = \overrightarrow {AA'} \], suy ra toạ độ điểm \[A'\] là \[\left( { - 2;0;4} \right)\].
Từ đó ta có \[\overrightarrow {A'B} = \left( {4;0; - 4} \right),\overrightarrow {A'C} = \left( {2;3; - 4} \right)\]. Vậy \[\overrightarrow u = \overrightarrow {A'B} + \overrightarrow {A'C} \] thì \[\overrightarrow u = \left( {6;3; - 8} \right)\].
c) Gọi \[C'\left( {a;b;c} \right) \Rightarrow \overrightarrow {CC'} = \left( {a;b - 3;c} \right)\].
Ta có \[\overrightarrow {BB'} = \overrightarrow {CC'} \], mà \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], suy ra toạ độ điểm \[C'\] là \[\left( { - 2;3;4} \right)\].
d) Hình chiếu vuông góc của điểm \[B\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[A\] (do \[Ox \bot \left( {Oyz} \right)\]).
Do \[Ox\,{\rm{//}}\,A'B'\] mà \[Ox \bot \left( {Oyz} \right)\] nên \[A'B' \bot \left( {Oyz} \right)\], từ đó suy ra hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[B'\].
Gọi \[{C_1}\left( {m;n;p} \right)\] là hình chiếu vuông góc của \[C'\] lên mặt phẳng \[\left( {Oyz} \right)\]\[ \Rightarrow {C_1}\left( {0;3;4} \right)\].
Vậy hình chiếu của hình lăng trụ \[ABC.A'B'C'\] lên mặt phẳng \[\left( {Oyz} \right)\]là hình chữ nhật \[AB'{C_1}C\].
Diện tích đa giác là: \[{S_{AB'{C_1}C}} = AB' \cdot AC = 4 \cdot 3 = 12\].
Đáp án: a) Sai, b) Đúng, c) Đúng, d) Sai.
Câu 2
Lời giải
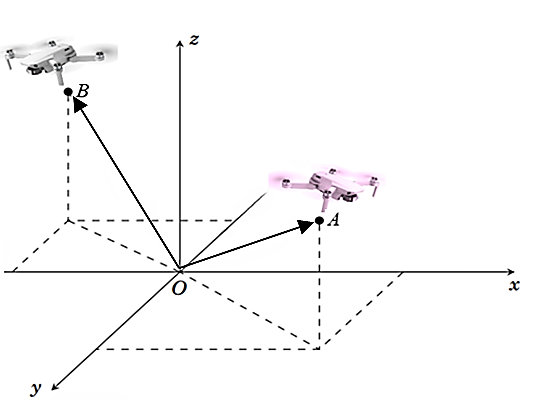
Ta có \[\vec u = 2\vec a - 3\vec b + \vec c = \left( {5\,;\,3\,;\, - 9} \right)\]. Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.