(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}x - y = 16\\2x - 5y = - 28\end{array} \right.\];
b) \[\left\{ \begin{array}{l}5x + 4y = 18\,\,040\\3x - 2y = 2\,\,002\end{array} \right..\]
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Từ phương trình thứ nhất ta có \[x - y = 16\] suy ra \(x = 16 + y\). Thế vào phương trình thứ hai, ta được:
\[2\left( {16 + y} \right) - 5y = - 28\], tức là \[32 - 3y = - 28\], suy ra \[3y = 60\] hay \[y = 20\].
Từ đó \[x = 16 + 20 = 36.\]
Vậy hệ phương trình đã cho có nghiệm là \[\left( {36;20} \right).\]
b) Từ phương trình thứ nhất ta có \[5x + 4y = 18\,\,040\] suy ra \(x = 3\,\,608 - \frac{4}{5}y\). Thế vào phương trình thứ hai, ta được:
\[3\left( {3608 - \frac{4}{5}y} \right) - 2y = 2002\], tức là \[10824 - \frac{{22}}{5}y = 2002\], suy ra \[\frac{{22}}{5}y = 8822\] hay \[y = 2005.\]
Từ đó \[x = 3608 - \frac{4}{5}.2005 = 2004.\]
Vậy hệ phương trình đã cho có nghiệm là \[\left( {2004\,;2005} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \(\frac{{x - 2}}{{2017}} + \frac{{x - 3}}{{2018}} < \frac{{x - 4}}{{2019}} + \frac{{x - 5}}{{2020}}\)
\(\frac{{x - 2}}{{2017}} + \frac{{x - 3}}{{2018}} + 2 < \frac{{x - 4}}{{2019}} + \frac{{x - 5}}{{2020}} + 2\)
\(\left( {\frac{{x - 2}}{{2017}} + 1} \right) + \left( {\frac{{x - 3}}{{2018}} + 1} \right) < \left( {\frac{{x - 4}}{{2019}} + 1} \right) + \left( {\frac{{x - 5}}{{2020}} + 1} \right)\)
\(\frac{{x - 2015}}{{2017}} + \frac{{x - 2015}}{{2018}} < \frac{{x - 2015}}{{2019}} + \frac{{x - 2015}}{{2020}}\)
\(\frac{{x - 2015}}{{2017}} + \frac{{x - 2015}}{{2018}} - \frac{{x - 2015}}{{2019}} - \frac{{x - 2015}}{{2020}} < 0\)
\(\left( {x - 2015} \right)\left( {\frac{1}{{2017}} + \frac{1}{{2018}} - \frac{1}{{2019}} - \frac{1}{{2020}}} \right) < 0\)
Nhận thấy \(\frac{1}{{2017}} + \frac{1}{{2018}} - \frac{1}{{2019}} - \frac{1}{{2020}} > 0\).
Do đó, để thỏa mãn yêu cầu bài toán thì \(x - 2015 < 0\) suy ra \(x < 2015.\)
Vậy \(x < 2015.\)
Câu 2
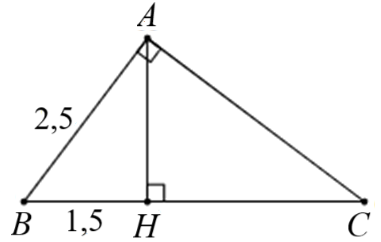
A. \(\widehat B = 30^\circ .\)
B. \(\widehat B = 53^\circ 1'.\)
C. \(\widehat B = 35^\circ 1'.\)
Lời giải
Đáp án đúng là: B
Tam giác \(ABH\) vuông tại \(H\), ta có: \[\cos B = \frac{{BH}}{{AH}}\] hay \(\cos B = \frac{{1,5}}{{2,5}} = \frac{3}{5}\), suy ra \(\widehat B \approx 53^\circ 1'\).
Vậy chọn đáp án B.
Câu 3
(2,0 điểm)
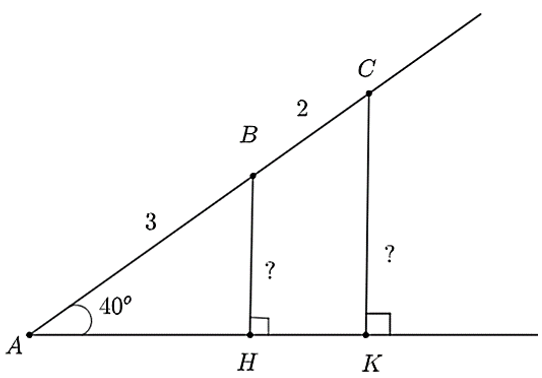
1) Cho hình vẽ dưới đây, tính độ dài các cạnh \(BH,CK,AK.\) (kết quả được làm tròn đến hàng phần mười).
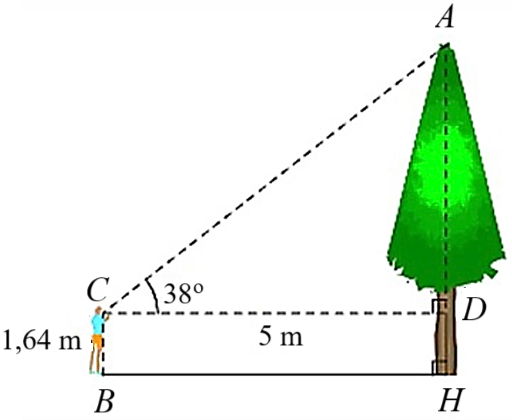
2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\left\{ \begin{array}{l}3x + 2y = 1\\x + y = 0\end{array} \right.\].
B. \[\left\{ \begin{array}{l}3x + 2y = 1\\x - y = 0\end{array} \right.\].
C. \[\left\{ \begin{array}{l}3x - 2y = 1\\x + y = 0\end{array} \right.\].
D. \[\left\{ \begin{array}{l}3x - 2y = 1\\x - y = 0\end{array} \right..\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(4,33\).
B. \({\rm{3,4}}{\rm{.}}\)
C. \({\rm{1,44}}{\rm{.}}\)
D. \(1,3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.