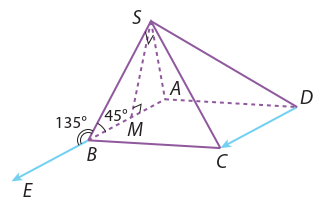
Trong không gian, cho hai vectơ \[\overrightarrow a \] và \[\overrightarrow b \] khác \[\overrightarrow 0 \]. Lấy điểm O và vẽ các vec tơ \[\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \]. Lấy điểm O’ khác O và vẽ các vec tơ \[\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \]
a) Giải thích vì sao \[\overrightarrow {AB} = \overrightarrow {A'B'} \]
b) Áp dụng định lí cosin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \[\widehat {AOB} = \widehat {A'O'B'}\].
Quảng cáo
Trả lời:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} ;\overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {{A^\prime }{O^\prime }} + \overrightarrow {{O^\prime }{B^\prime }} \)
Mà \(\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b,\overrightarrow {{O^\prime }{A^\prime }} = \vec a,\overrightarrow {{O^\prime }{B^\prime }} = \vec b \Rightarrow \overrightarrow {AO} = \overrightarrow {{A^\prime }{O^\prime }} ;\overrightarrow {OB} = \overrightarrow {{O^\prime }{B^\prime }} \)
Do đó, \(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} \)
b) Áp dụng định lí côsin vào tam giác AOB ta có: \(\cos AOB = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA \cdot OB}}\)
Áp dụng định lí côsin vào tam giác \({{\rm{A}}^\prime }{A^\prime }{B^\prime }\) ta có: \(\cos {A^\prime }{O^\prime }{B^\prime } = \frac{{{O^\prime }{A^{\prime 2}} + {O^\prime }{B^2} - {A^\prime }{B^2}}}{{2 \cdot {O^\prime }{A^\prime } \cdot {O^\prime }{B^\prime }}}\)
vi \(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} \Rightarrow AB = {A^\prime }{B^\prime },\overrightarrow {AO} = \overrightarrow {{A^\prime }{O^\prime }} \Rightarrow OA = {O^\prime }{A^\prime };\overrightarrow {OB} = \overrightarrow {{O^\prime }{B^\prime }} \Rightarrow OB = {O^\prime }{B^\prime }\)
Do đó, \(\cos AOB = \cos {A^\prime }{O^\prime }{B^\prime } \Rightarrow AOB = {A^\prime }{O^\prime }{B^\prime }\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
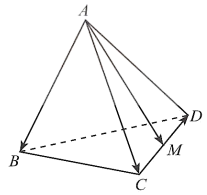
a) Ta có:
Tương tự ta cūng có \(\overrightarrow {AB} \cdot \overrightarrow {AD} = \frac{{{a^2}}}{2}\).
Ta lại có \(\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AC} + \overrightarrow {AD} )\), suy ra:
\[\overrightarrow {AB} .\overrightarrow {AM} = \overrightarrow {AB} .\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AD} } \right) = \frac{1}{2}\left( {\frac{{{a^2}}}{2} + \frac{{{a^2}}}{2}} \right) = \frac{{{a^2}}}{2}\]
b) Ta có: \[\overrightarrow {AB} .\overrightarrow {CD} = \left( {\overrightarrow {AM} + \overrightarrow {MB} } \right)\overrightarrow {CD} = \overrightarrow {AM} .\overrightarrow {CD} + \overrightarrow {MB} .\overrightarrow {CD} \]
Mà AM, BM là trung tuyến của các tam giác đều ACD, BCD nên \(\overrightarrow {AM} \bot \overrightarrow {CD} ,\overrightarrow {MB} \bot \overrightarrow {CD} \).
Suy ra \(\overrightarrow {AM} \cdot \overrightarrow {CD} = \overrightarrow {MB} \cdot \overrightarrow {CD} = 0\).
Từ các kết quả trên ta có \(\overrightarrow {AB} \cdot \overrightarrow {CD} = 0\). Suy ra
Lời giải
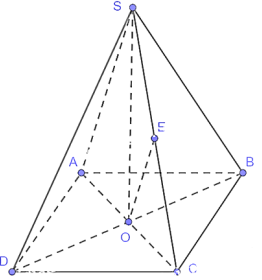
a) Tam giác SAD có ba cạnh bằng nhau nên là tam giác đều, suy ra . Tứ giác ABCD là hình vuông nên \(\overrightarrow {AD} = \overrightarrow {BC} \), suy ra . Do đó
b) Tứ giác ABCD là hình vuông có độ dài mỗi cạnh là a nên độ dài đường chéo AC là \(\sqrt 2 a\). Tam giác SAC có \(SA = SC = a\) và \(AC = \sqrt 2 a\) nên tam giác SAC vuông cân tại \(S\), suy ra . Do đó .
c) Gọi \({\rm{O}}\) là giạo điểm của hai đường chéo \({\rm{AC}}\) và \({\rm{BD}}\) trong hình vuông \({\rm{ABCD}}\). Do đó, \({\rm{O}}\) là trung diểm của \({\rm{BD}},{\rm{O}}\) là trung diếm của \({\rm{AC}}\).
Tứ giác \({\rm{ABCD}}\) là hình vuông cạnh a nên độ dài đường chéo \({\rm{BD}}\) là
Gọi \({\rm{E}}\) là trung điểm của \({\rm{SC}}\). Mà \({\rm{O}}\) là trung diểm của \({\rm{AC}}\) nên \({\rm{OE}}\) là đường trung bình của tam giác \({\rm{SAC}}\), do đó, \({\rm{OE}}//{\rm{SA}},OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS} = 2\overrightarrow {OE} \)
Vì \({\rm{O}}\) là trung diểm của \({\rm{BD}}\) nên \(\overrightarrow {BD} = 2\overrightarrow {OB} \)
Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, $B E$ là đường trung tuyến đồng thời là đường cao của tam giác \({\rm{SBC}}\). Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên EOB vuông tại \({\rm{O}}\). Do đó, \(\overrightarrow {OE} \bot \overrightarrow {OB} \)
Ta có: \(\overrightarrow {AS} \cdot \overrightarrow {BD} = 2\overrightarrow {OE} \cdot ( - 2\overrightarrow {OB} ) = - 4\overrightarrow {OE} \cdot \overrightarrow {OB} = 0\)
d) Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
Ta có: \(\overrightarrow {AS} \cdot \overrightarrow {CD} = \overrightarrow {AS} \cdot \overrightarrow {BA} = - \overrightarrow {AS} \cdot \overrightarrow {AB} = - |\overrightarrow {AS} | \cdot |\overrightarrow {AB} |\cos (\overrightarrow {AS} ,\overrightarrow {AB} ) = - |\overrightarrow {AS} | \cdot |\overrightarrow {AB} |\cos SAB\)
Vì tam giác \({\rm{SAB}}\) có ba cạnh bằng nhau nên tam giác \({\rm{SAB}}\) dều, suy ra
Suy ra:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.