12 bài tập Góc giữa hai vectơ trong không gian – Tích vô hướng (có lời giải)
36 người thi tuần này 4.6 334 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
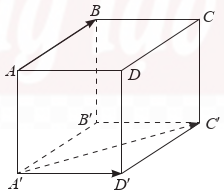
Ta có \[\overrightarrow {AD} \; = \overrightarrow {A'D'} \], suy ra \[\left( {\overrightarrow {AB} ,\overrightarrow {A'D'} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \overrightarrow {DAB} = {90^ \circ }\].
Ta có \[\overrightarrow {A'C'} \; = \overrightarrow {AC} \], suy ra \[\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \overrightarrow {CAB} = {45^ \circ }\]Lời giải
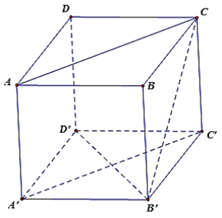
Vì \(A{A^\prime }//C{C^\prime }\) và \(A{A^\prime } = C{C^\prime }\) nên \(A{A^\prime }{C^\prime }C\) là hình bình hành.
Suy ra \(\overrightarrow {AC} = \overrightarrow {{A^\prime }{C^\prime }} \).
Vì AA'B'B là hình vuông nên \(\overrightarrow {{A^\prime }A} = \overrightarrow {{B^\prime }B} \).
Do đó
(Vì \(B{B^\prime }{C^\prime }C\) là hình vuông nên \({B^\prime }C\) là phân giác của \(B{B^\prime }{C^\prime }\) ).
Lời giải
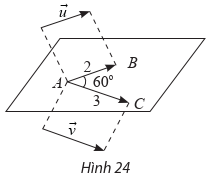
a) Vì \(\overrightarrow {AB} = \vec u,\overrightarrow {AC} = \vec v\) nên
b) \(|\vec u| = 2,|\vec v| = 3\) nên \(|\overrightarrow {AB} | = 2,|\overrightarrow {AC} | = 3\).
Ta có
Lời giải
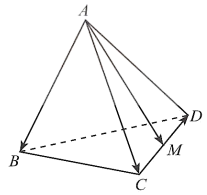
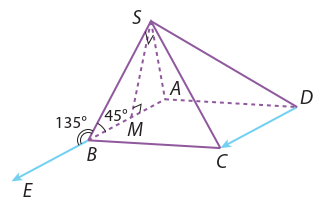
a) Ta có:
Tương tự ta cūng có \(\overrightarrow {AB} \cdot \overrightarrow {AD} = \frac{{{a^2}}}{2}\).
Ta lại có \(\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AC} + \overrightarrow {AD} )\), suy ra:
\[\overrightarrow {AB} .\overrightarrow {AM} = \overrightarrow {AB} .\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AD} } \right) = \frac{1}{2}\left( {\frac{{{a^2}}}{2} + \frac{{{a^2}}}{2}} \right) = \frac{{{a^2}}}{2}\]
b) Ta có: \[\overrightarrow {AB} .\overrightarrow {CD} = \left( {\overrightarrow {AM} + \overrightarrow {MB} } \right)\overrightarrow {CD} = \overrightarrow {AM} .\overrightarrow {CD} + \overrightarrow {MB} .\overrightarrow {CD} \]
Mà AM, BM là trung tuyến của các tam giác đều ACD, BCD nên \(\overrightarrow {AM} \bot \overrightarrow {CD} ,\overrightarrow {MB} \bot \overrightarrow {CD} \).
Suy ra \(\overrightarrow {AM} \cdot \overrightarrow {CD} = \overrightarrow {MB} \cdot \overrightarrow {CD} = 0\).
Từ các kết quả trên ta có \(\overrightarrow {AB} \cdot \overrightarrow {CD} = 0\). Suy ra
Lời giải
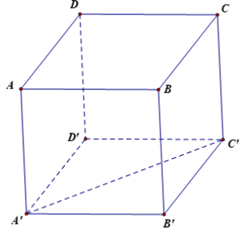
a) Vì ABB'A' là hình vuông nên \(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} \).
Do đó (do \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình vuông nên \({A^\prime }{C^\prime }\) là̀ phân giác của góc \(\left. {{D^\prime }{A^\prime }{B^{\prime \prime }}} \right)\).
Ví \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình vuông cạnh bẳng 1 nên \({A^\prime }{C^\prime } = \sqrt 2 \).
Ta có
Vì \({\rm{AC}}{{\rm{C}}^\prime }{A^\prime }\) là hình bình hành nên \(\overrightarrow {C{C^\prime }} = \overrightarrow {A{A^\prime }} \).
Do đó
Do đó \(\overrightarrow {AB} \bot \overrightarrow {C{C^\prime }} \). Suy ra \(\overrightarrow {AB} \cdot \overrightarrow {C{C^\prime }} = 0\).
b) \(\left( {\overrightarrow {AC} ,\overrightarrow {A{C^\prime }} } \right) = CA{C^\prime }\).
Ta có \(A{C^\prime }\) là đường chéo của hình lập phương cạnh bẳng 1 nên \(A{C^\prime } = \sqrt 3 \).
\({\rm{AC}}\) là đường chéo của hình vuông \({\rm{ABCD}}\) cạnh bằng 1 nên \(AC = \sqrt 2 \).
Xét \({\rm{DACC}}\) có
Vậy
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.