Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn \(28\,{\rm{cm}}\), trục nhỏ \(25\,{\rm{cm}}\). Biết cứ \(1000\,{\rm{c}}{{\rm{m}}^3}\) dưa hấu sẽ làm được cốc sinh tố giá \(20000\) đồng. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn \(28\,{\rm{cm}}\), trục nhỏ \(25\,{\rm{cm}}\). Biết cứ \(1000\,{\rm{c}}{{\rm{m}}^3}\) dưa hấu sẽ làm được cốc sinh tố giá \(20000\) đồng. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
A. \(183000\) đồng.
B. \(180000\) đồng.
C. \(185000\) đồng.
D. \(190000\) đồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Đường elip có trục lớn \(28\,{\rm{cm}}\), trục nhỏ \(25\,{\rm{cm}}\) có phương trình \( + \frac{{{y^2}}}{{{{\left( {\frac{{25}}{2}} \right)}^2}}} = 1\)\( \Leftrightarrow {y^2} = {\left( {\frac{{25}}{2}} \right)^2}\left( {1 - \frac{{{x^2}}}{{{{14}^2}}}} \right)\)\( \Leftrightarrow y = \pm \frac{{25}}{2}\sqrt {1 - \frac{{{x^2}}}{{{{14}^2}}}} \).
Do đó thể tích quả dưa là \[V = \pi \int\limits_{ - 14}^{14} {{{\left( {\frac{{25}}{2}\sqrt {1 - \frac{{{x^2}}}{{{{14}^2}}}} } \right)}^2}{\rm{d}}x} \]\( = \pi {\left( {\frac{{25}}{2}} \right)^2}\int\limits_{ - 14}^{14} {{{\left( {1 - \frac{{{x^2}}}{{{{14}^2}}}} \right)}^2}{\rm{d}}x} \)\( = \pi {\left( {\frac{{25}}{2}} \right)^2}.\left. {\left( {x - \frac{{{x^3}}}{{{{3.14}^2}}}} \right)} \right|_{ - 14}^{14}\)\( = \pi {\left( {\frac{{25}}{2}} \right)^2}.\frac{{56}}{3}\)\( = \frac{{8750\pi }}{3}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Do đó tiền bán nước thu được là \(\frac{{8750\pi .20000}}{{3.1000}} \approx 183259\,\)đồng.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.105660667đ
B.1066666667đ
C.107665667đ
D.108665667đ
Lời giải
Chọn B
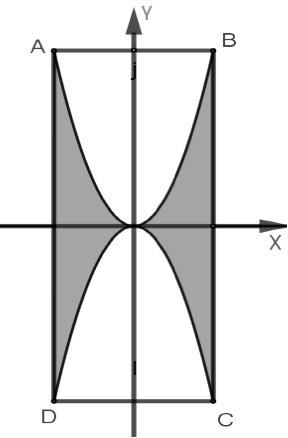
Vì \(AB = 4dm;BC = 8dm.\)\( \Rightarrow A( - 2;4),\)\(B(2;4),C(2; - 4),D( - 2; - 4)\).
parabol là: \(y = {x^2}\) hoặc \(y = - {x^2}\)
Diện tích phần tô đậm là \[{S_1} = 4\int\limits_0^2 {{x^2}dx = \frac{{32}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})} \]
Diện tích hình chữ nhật là \[S = 4.8 = 32\begin{array}{*{20}{c}}{}\end{array}({m^2})\]
Diện tích phần trắng là \[{S_2} = S - {S_1} = 32 - \frac{{32}}{3} = \frac{{64}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})\]
Tổng chi phí trang chí là:
Câu 2
A. \(110\) triệu đồng.
B. \(250\) triệu đồng.
C. \(180\) triệu đồng.
D. \(200\) triệu đồng.
Lời giải
Chọn D
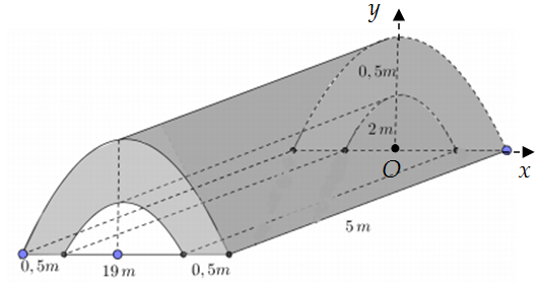
Chọn hệ trục \[Oxy\] như hình vẽ.
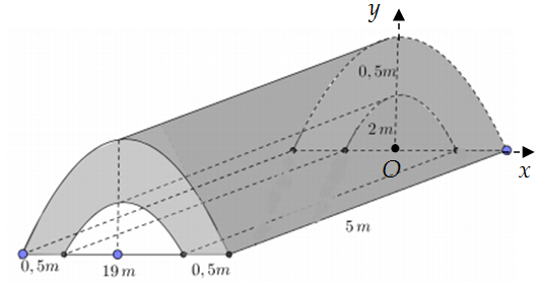
Gọi \[\left( {{P_1}} \right):y = {a_1}{x^2} + {b_1}\] là Parabol đi qua hai điểm \[A\left( {\frac{{19}}{2};0} \right),B\left( {0;2} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = a.{\left( {\frac{{19}}{2}} \right)^2} + 2\\2 = b\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = - \frac{8}{{361}}\\{b_1} = 2\end{array} \right.\]\[ \Rightarrow \left( {{P_1}} \right):y = - \frac{8}{{361}}{x^2} + 2\].
Gọi \[\left( {{P_2}} \right):y = {a_2}{x^2} + {b_2}\] là Parabol đi qua hai điểm \[C\left( {10;0} \right),D\left( {0;\frac{5}{2}} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = {a_2}.{\left( {10} \right)^2} + \frac{5}{2}\\\frac{5}{2} = {b_2}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_2} = - \frac{1}{{40}}\\{b_2} = \frac{5}{2}\end{array} \right.\]\[ \Rightarrow \left( {{P_2}} \right):y = - \frac{1}{{40}}{x^2} + \frac{5}{2}\].
Ta có thể tích của bê tông là: \[V = 5.2\left[ {\int_0^{10} {\left( { - \frac{1}{{40}}{x^2} + \frac{5}{2}} \right)} {\rm{d}}x - \int_0^{\frac{{19}}{2}} {\left( { - \frac{8}{{361}}{x^2} + 2} \right)} {\rm{d}}x} \right] = 40\,{{\rm{m}}^3}\].
Số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu là: \[5.40 = 200\] triệu đồng
Câu 3
A. \(800\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
B. \[\frac{{800}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
C. \(\frac{{400}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
D. \(250\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(30\;{m^3}\)
B. \(36\;{m^3}\)
C. \(40\;{m^3}\)
D. \(41\;{m^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(240\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
B. \(240\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
C. \(120\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
D. \(120\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho một mô hình [3D] mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid13-1753788326.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo