Một thiết bị thăm dò đáy biển đang lặn với vận tốc \[\overrightarrow v \]= (10; 8; –3) (Hình vẽ). Cho biết vận tốc của dòng hải lưu của vùng biển là \[\overrightarrow w \] = (3,5; 1; 0).
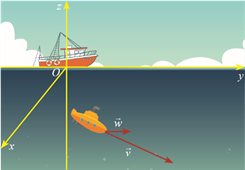
a) Tìm toạ độ của vectơ tổng hai vận tốc \[\overrightarrow v \] và \[\overrightarrow w \].
b) Giả sử thiết bị thăm dò lặn với vận tốc \[\overrightarrow u \]= (7; 2; 0), hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.

a) Tìm toạ độ của vectơ tổng hai vận tốc \[\overrightarrow v \] và \[\overrightarrow w \].
b) Giả sử thiết bị thăm dò lặn với vận tốc \[\overrightarrow u \]= (7; 2; 0), hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.
Quảng cáo
Trả lời:
a) \(\vec v + \vec w = (10 + 3,5;8 + 1; - 3 + 0) = (13,5;9; - 3)\).
b) \(\vec u = (7;2;0) = 2(3,5;1;0) = 2\vec w\).
Do đó hai vectơ này cùng phương, cùng hướng với nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
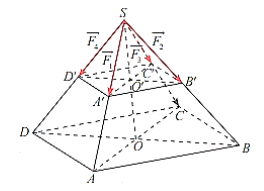
Lời giải
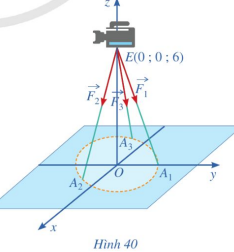
Theo giả thiết, ta có các diếm \({\rm{E}}(0;0;6),{{\rm{A}}_1}(0;1;0),{A_2}\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right),{A_3}\left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right)\).
Suy ra \(\overline {{\rm{E}}{{\rm{A}}_1}} = (0 - 0;1 - 0;0 - 6)\) hay \(\overrightarrow {{\rm{E}}{{\rm{A}}_1}} = (0;1; - 6)\);
\(\overrightarrow {{\rm{E}}{{\rm{A}}_2}} = \left( {\frac{{\sqrt 3 }}{2} - 0; - \frac{1}{2} - 0;0 - 6} \right){\rm{ hay }}\overrightarrow {{\rm{E}}{{\rm{A}}_2}} = \left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 6} \right);\)
\({\rm{ }}\overrightarrow {{\rm{E}}{{\rm{A}}_3}} = \left( { - \frac{{\sqrt 3 }}{2} - 0; - \frac{1}{2} - 0;0 - 6} \right){\rm{ hay }}\overrightarrow {{\rm{E}}{{\rm{A}}_3}} = \left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 6} \right).\)
Vî vậy, tồn tại hằng số \({\rm{c}} \ne 0\) sao cho:
\(\overrightarrow {{F_1}} = \overrightarrow {E{A_1}} = (0;c; - 6c);\overrightarrow {{F_2}} = \overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2}c; - \frac{1}{2}c; - 6c} \right);\overrightarrow {{F_3}} = c\overrightarrow {E{A_3}} = \left( { - \frac{{\sqrt 3 }}{2}c; - \frac{1}{2}c; - 6c} \right).\)
Suy ra \({\vec F_1} + {\vec F_2} + {\vec F_3} = (0;0; - 18c)\).
Mặt khác, ta có: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec F\), trong đó \(\vec F = (0;0; - 300)\) là trọng lực tác dụng lên máy quay. Suy ra \(18{\rm{c}} = - 300\), tức là \({\rm{c}} = \frac{{50}}{3}\).
Vậy: \({\vec F_1} = \left( {0;\frac{{50}}{3}; - 100} \right);\overrightarrow {{F_2}} = \left( {\frac{{25\sqrt 3 }}{3};\frac{{ - 25}}{3}; - 100} \right);{\vec F_3} = \left( {\frac{{ - 25\sqrt 3 }}{3};\frac{{ - 25}}{3}; - 100} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.