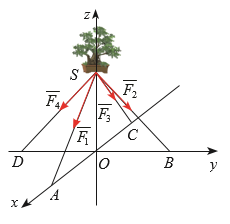
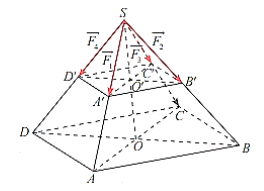
Một chậu cây được đặt trên một giá đỡ có bốn chân với điểm đặt S(0; 0; 20) và các điểm chạm mặt đất của bốn chân lần lượt là A(20; 0; 0), B(0; 20; 0), C(–20; 0; 0), D(0; –20; 0) (đơn vị cm). Cho biết trọng lực tác dụng lên chậu cây có độ lớn 40 N và được phân bố thành bốn lực \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \] có độ lớn bằng nhau như Hình 4. Tìm toạ độ của các lực nói trên (mỗi centimét biểu diễn 1 N).

Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
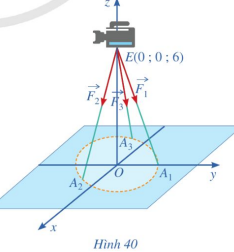
Theo giả thiết, ta có các diếm \({\rm{E}}(0;0;6),{{\rm{A}}_1}(0;1;0),{A_2}\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right),{A_3}\left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right)\).
Suy ra \(\overline {{\rm{E}}{{\rm{A}}_1}} = (0 - 0;1 - 0;0 - 6)\) hay \(\overrightarrow {{\rm{E}}{{\rm{A}}_1}} = (0;1; - 6)\);
\(\overrightarrow {{\rm{E}}{{\rm{A}}_2}} = \left( {\frac{{\sqrt 3 }}{2} - 0; - \frac{1}{2} - 0;0 - 6} \right){\rm{ hay }}\overrightarrow {{\rm{E}}{{\rm{A}}_2}} = \left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 6} \right);\)
\({\rm{ }}\overrightarrow {{\rm{E}}{{\rm{A}}_3}} = \left( { - \frac{{\sqrt 3 }}{2} - 0; - \frac{1}{2} - 0;0 - 6} \right){\rm{ hay }}\overrightarrow {{\rm{E}}{{\rm{A}}_3}} = \left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 6} \right).\)
Vî vậy, tồn tại hằng số \({\rm{c}} \ne 0\) sao cho:
\(\overrightarrow {{F_1}} = \overrightarrow {E{A_1}} = (0;c; - 6c);\overrightarrow {{F_2}} = \overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2}c; - \frac{1}{2}c; - 6c} \right);\overrightarrow {{F_3}} = c\overrightarrow {E{A_3}} = \left( { - \frac{{\sqrt 3 }}{2}c; - \frac{1}{2}c; - 6c} \right).\)
Suy ra \({\vec F_1} + {\vec F_2} + {\vec F_3} = (0;0; - 18c)\).
Mặt khác, ta có: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec F\), trong đó \(\vec F = (0;0; - 300)\) là trọng lực tác dụng lên máy quay. Suy ra \(18{\rm{c}} = - 300\), tức là \({\rm{c}} = \frac{{50}}{3}\).
Vậy: \({\vec F_1} = \left( {0;\frac{{50}}{3}; - 100} \right);\overrightarrow {{F_2}} = \left( {\frac{{25\sqrt 3 }}{3};\frac{{ - 25}}{3}; - 100} \right);{\vec F_3} = \left( {\frac{{ - 25\sqrt 3 }}{3};\frac{{ - 25}}{3}; - 100} \right)\)
Lời giải
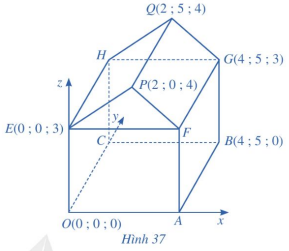
a) Ta có \(\overrightarrow {AB} = (4;6;8);\overrightarrow {AC} = (8;10;3);\overrightarrow {BC} = (4;4; - 5)\).
Khi đó: \(|\overrightarrow {AB} | = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \);
\(|\overrightarrow {AC} | = \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} ;{\rm{ }}\overrightarrow {BC} = \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
b) Ta có
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.