Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24 m, \(\widehat {CAD} = 63^\circ \); \(\widehat {CBD} = 48^\circ \).
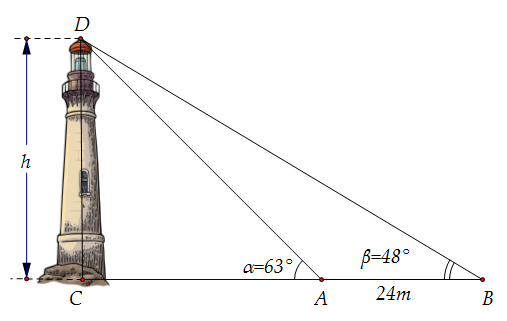
Chiều cao h của khối tháp gần với giá trị nào sau đây?
A. 61,4 m.
B. 18,5 m.
C. 60 m.
D. 18 m.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có \(\widehat {CAD} = 63^\circ \Rightarrow \widehat {BAD} = 117^\circ \Rightarrow \widehat {ADB} = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \).
Áp dụng định lý sin trong tam giác ABD ta có: \(\frac{{AB}}{{\sin \widehat {ADB}}} = \frac{{BD}}{{\sin \widehat {BAD}}} \Rightarrow BD = \frac{{AB \cdot \sin \widehat {BAD}}}{{\sin \widehat {ADB}}}\).
Tam giác BCD vuông tại C nên có: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}} \Rightarrow CD = BD \cdot \sin \widehat {CBD}\).
Vậy \[CD = \frac{{AB \cdot \sin \widehat {BAD} \cdot \sin \widehat {CBD}}}{{\sin \widehat {ADB}}} = \frac{{24 \cdot \sin 117^\circ \cdot sin48^\circ }}{{\sin 15^\circ }} = 61,4\,\,{\rm{(m)}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
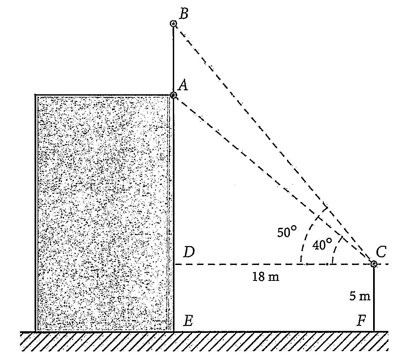
Trong tam giác \(DAC\), ta có:
\(\cos \widehat {ACD} = \frac{{DC}}{{AC}}\), suy ra \(AC = \frac{{DC}}{{\cos A}} = \frac{{18}}{{\cos 40^\circ }} \approx 23,5\,{\rm{m}}\).
Trong tam giác \(DBC\) ta có:
\(\cos \widehat {BCD} = \frac{{DC}}{{BC}}\), suy ra \(BC = \frac{{DC}}{{\cos B}} = \frac{{18}}{{\cos 50^\circ }} \approx 28\,\;{\rm{m}}\).
Lại có góc \(\widehat {ACB} = 50^\circ - 40^\circ = 10^\circ \), áp dụng định lí côsin trong tam giác \(ABC\), ta có:
\(AB = \sqrt {C{A^2} + C{B^2} - 2CA \cdot CB \cdot \cos \widehat {ACB}} \) \( \approx \sqrt {23,{5^2} + {{28}^2} - 2 \cdot 23,5 \cdot 28 \cdot \cos 10^\circ } \approx 6,34\,{\rm{m}}.\)
Vậy chiều cao của cột cờ (làm tròn đến hàng phần trăm là) 6,34 m.
Đáp án: 6,34.
Lời giải
Lời giải
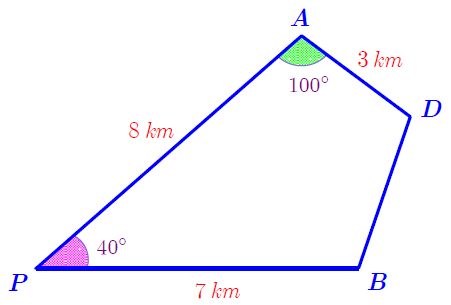
Xét tam giác \[PAD\] có
\[PD = \sqrt {P{A^2} + A{D^2} - 2 \cdot PA \cdot AD \cdot \cos \widehat {PAD}} = \sqrt {{8^2} + {3^2} - 2 \cdot 8 \cdot 3 \cdot \cos 100^\circ } \approx 9,02\],
và \[\cos \widehat {APD} = \frac{{P{A^2} + P{D^2} - A{D^2}}}{{2 \cdot PA \cdot PD}} = \frac{{{8^2} + 9,{{02}^2} - {3^2}}}{{2 \cdot 8 \cdot 9,02}} \approx 0,94\] suy ra \[\widehat {APD} \approx 19^\circ \].
Xét tam giác \[PBD\] có \[\widehat {BPD} = \widehat {BPA} - \widehat {APD} \approx 40^\circ - 19^\circ = 21^\circ \],
và \[BD = \sqrt {P{B^2} + P{D^2} - 2 \cdot PB \cdot PD \cdot \cos \widehat {BPD}} \] \[ \approx 3,53\] (km).
Vậy bạn Bình phải đi khoảng \[3,53\] km nữa để đến đích.
Đáp án: \(3,53\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\sqrt {94} \).
B. \[\sqrt {106} \].
C. \(\sqrt {166} \).
D. \[\sqrt {34} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.