Câu hỏi:
12/07/2024 54,763Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Câu hỏi trong đề: Giải toán 8: Chương 1: Tứ giác !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
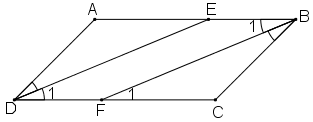
a) Ta có:
+ ABCD là hình bình hành ⇒ AB // CD ⇒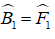 
(Hai góc đồng vị) (1)
+ DE là tia phân giác của góc D
Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)
b) Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
⇒ DEBF là hình bình hành.
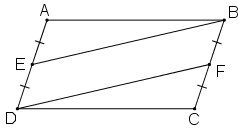
Lời giải
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = \(\frac{{AD}}{2}\)
F là trung điểm của BC ⇒ CF = \(\frac{{BC}}{2}\)
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Trần Đạt
cho tam giác bcd vuông tại c (bc bé hơn dc) có đường cao ck gọi i là trung điểm cd. trên tia đối tia ik lấy m sao cho ik bằng im
Nguyễn Hòa
Dạ e có thắc mắc là tại sao ak=kn,am//kn thì bn=mn ạ?
Xem tất cả 1 phản hồi
SieuNhan
Trong đường trung bình của lớp 8 hay sao ý bạn