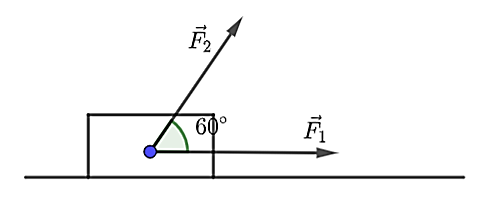
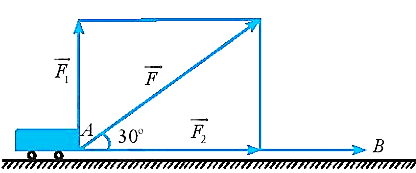
Hai người cùng kéo một xe goòng. Người thứ nhất và người thứ hai lần lượt tác dụng vào chiếc xe goòng bằng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hai lực vuông góc nhau, phương lực \(\overrightarrow {{F_2}} \) song song mặt đường) như hình vẽ và lực tổng hợp hợp với phương ngang (mặt đường) một góc \(30^\circ \). Người thứ nhất kéo một lực là \[40\sqrt 3 \] (N), người thứ hai kéo một lực là \[80\] (N).

a) \(\left| {\overrightarrow {{F_1}} } \right| = 80,\left| {\overrightarrow {{F_2}} } \right| = 40\sqrt 3 \).

b) \(\left( {\overrightarrow {{F_2}} ,\overrightarrow F } \right) = 30^\circ \).

c) Độ lớn của \(\overrightarrow F \) bằng \(40\sqrt 7 \) (N).

d) Công sinh ra khi kéo vật đi một khoảng dài \(50\) (m) là \(a\sqrt b \) (J) thì tổng \(a + b = 1021\).

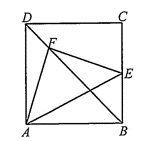
a) Đúng. Ta có \(\overrightarrow {AE}  = \overrightarrow {AB}  + \overrightarrow {BE}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {BC}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AD} \).

b) Sai. \(\overrightarrow {AF}  = \overrightarrow {AB}  + \overrightarrow {BF}  = \overrightarrow {AB}  + \frac{3}{4}\overrightarrow {BD}  = \overrightarrow {AB}  + \frac{3}{4}\left( {\overrightarrow {AD}  - \overrightarrow {AB} } \right) = \frac{1}{4}\overrightarrow {AB}  + \frac{3}{4}\overrightarrow {AD} .\)

c) Đúng. \(\overrightarrow {EF}  = \overrightarrow {AF}  - \overrightarrow {AE}  = \left( {\frac{1}{4}\overrightarrow {AB}  + \frac{3}{4}\overrightarrow {AD} } \right) - \left( {\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AD} } \right) = \frac{{ - 3}}{4}\overrightarrow {AB}  + \frac{1}{4}\overrightarrow {AD} .\)

d) Đúng. Ta có \(\overrightarrow {AF}  \cdot \overrightarrow {EF}  = \left( {\frac{1}{4}\overrightarrow {AB}  + \frac{3}{4}\overrightarrow {AD} } \right) \cdot \left( {\frac{{ - 3}}{4}\overrightarrow {AB}  + \frac{1}{4}\overrightarrow {AD} } \right)\)

                                        \( = \frac{{ - 3}}{{16}}{\overrightarrow {AB} ^2} - \frac{1}{2}\overrightarrow {AB}  \cdot \overrightarrow {AD}  + \frac{3}{{16}}{\overrightarrow {AD} ^2} = 0 \Rightarrow AF \bot EF{\rm{. }}\)

Ta có \({\overrightarrow {AF} ^2} = {\left( {\frac{1}{4}\overrightarrow {AB}  + \frac{3}{4}\overrightarrow {AD} } \right)^2} = \frac{1}{{16}}{\overrightarrow {AB} ^2} + \frac{3}{8}\overrightarrow {AB}  \cdot \overrightarrow {AD}  + \frac{9}{{16}}{\overrightarrow {AD} ^2} = \frac{5}{8}{\overrightarrow {AB} ^2}\).

\({\overrightarrow {EF} ^2} = {\left( {\frac{{ - 3}}{4}\overrightarrow {AB}  + \frac{1}{4}\overrightarrow {AD} } \right)^2} = \frac{9}{{16}}{\overrightarrow {AB} ^2} - \frac{3}{8}\overrightarrow {AB}  \cdot \overrightarrow {AD}  + \frac{1}{{16}}{\overrightarrow {AD} ^2} = \frac{5}{8}{\overrightarrow {AB} ^2}.\)

\( \Rightarrow {\overrightarrow {AF} ^2} = {\overrightarrow {EF} ^2} = \frac{5}{8}{\overrightarrow {AB} ^2} \Rightarrow AF = EF\). Vậy tam giác \(AEF\) vuông cân tại \(F\).

Ta có \[\overrightarrow a  \cdot \overrightarrow b  = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 3 \cdot 2 \cdot \cos 120^\circ  =  - 3\].

\[{\left| {\overrightarrow a  - 2\overrightarrow b } \right|^2} = {\left( {\overrightarrow a  - 2\overrightarrow b } \right)^2} = {\overrightarrow a ^2} - 4\overrightarrow a  \cdot \overrightarrow b  + 4{\overrightarrow b ^2} = {\left| {\overrightarrow a } \right|^2} - 4\overrightarrow a  \cdot \overrightarrow b  + 4{\left| {\overrightarrow b } \right|^2} = {3^2} - 4 \cdot \left( { - 3} \right) + 4 \cdot {2^2} = 37\]

\[ \Rightarrow \left| {\overrightarrow a  - 2\overrightarrow b } \right| = \sqrt {37}  \approx 6,1\].

Đáp án: 6,1.