Trên mặt đất phả̉ng, người ta dựng một cây cột thẩng cao 6 m vuông góc với mặt đất, có chân cột đặt tại vị trí \(O\) trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉhh cột dưới mặt đất cách chân cột 3 m về hướng (hướng tạo với hướng nam góc và tạo với hướng đông góc (H.5.32). Chọn hệ trục Oxyz có gó́c toạ độ là O , tia Ox chi hướng nam, tia Oy chi hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trinh đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.
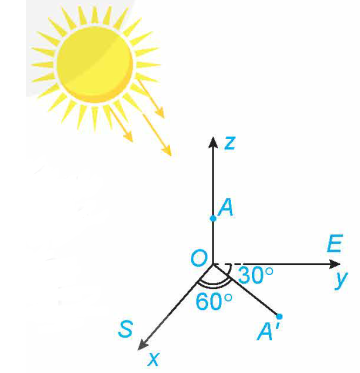
Trên mặt đất phả̉ng, người ta dựng một cây cột thẩng cao 6 m vuông góc với mặt đất, có chân cột đặt tại vị trí \(O\) trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉhh cột dưới mặt đất cách chân cột 3 m về hướng (hướng tạo với hướng nam góc và tạo với hướng đông góc (H.5.32). Chọn hệ trục Oxyz có gó́c toạ độ là O , tia Ox chi hướng nam, tia Oy chi hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trinh đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.

Quảng cáo
Trả lời:
Đế viết được phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điếm đang xét ta cần xác định tọa độ của A (đỉnh cột) và \({{\rm{A}}^\prime }\) (bóng của đỉnh cột).
Ta có \(A(0;0;6)\).
Hoành độ của điếm A' là
Tung độ của điếm \({{\rm{A}}^\prime }\) là
Do đó \({A^\prime }\left( {\frac{1}{2};\frac{{3\sqrt 3 }}{2};0} \right)\).
Đường thắng chứa tia nắng mặt trời đi qua \({\rm{A}}(0;0;6)\) và có vectơ chỉ phương \(\overrightarrow {A{A^\prime }} = \left( {\frac{1}{2};\frac{{3\sqrt 3 }}{2}; - 6} \right)\) có phương trình là: \(\left\{ {\begin{array}{*{20}{l}}{x = \frac{1}{2}t}\\{y = \frac{{3\sqrt 3 }}{2}t}\\{z = 6 - 6t}\end{array}} \right.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
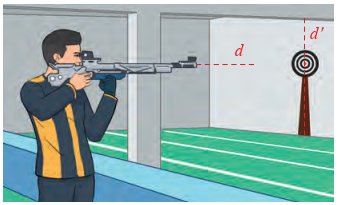
Đường thắng d và d' lần lượt có vectơ chỉ phương là \(\vec a = (1;0;0),\overrightarrow {{a^\prime }} = (0;0;3)\)
Ta có \(\vec a \cdot \overrightarrow {{a^\prime }} = 1.0 + 0.0 + 0.3 = 0\). Do đó d và d' vuông góc với nhau.
Lời giải
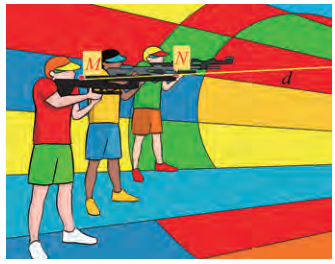
Ta có \(\overrightarrow {MN} = (0;1;0)\)
Đường thẳng MN đi qua \({\rm{M}}(3;3;1,5)\) và nhận \(\overrightarrow {MN} = (0;1;0)\) làm vectơ chỉ phương có phương trình là \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 3 + t}\\{z = 1,5}\end{array}} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.