Cho mặt phẳng \((\alpha ):\,\,2x\,\, - \,\,y\,\, + \,\,2z\,\, - \,\,1\,\, = \,\,0;\,\,(\beta ):\,\,x\,\, + \,\,2y\,\, - \,\,2z\,\, - \,\,3\,\, = \,\,0\). Cosin góc giữa mặt phẳng \((\alpha )\)và mặt phẳng\(\,(\beta )\) bằng:
A.\(\frac{4}{9}\)
B. \( - \frac{4}{9}.\)
C.\(\frac{4}{{3\sqrt 3 }}.\)
D. \( - \frac{4}{{3\sqrt 3 }}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Gọi \(\overrightarrow {{n_\alpha }} \), \(\,\overrightarrow {{n_\beta }} \) lần lượt là vectơ pháp tuyến của mặt phẳng \((\alpha )\) và \((\beta )\).
Ta có \(\overrightarrow {{n_\alpha }} (2;\,\, - \,\,1;\,\,2);\,\,\overrightarrow {{n_\beta }} (1;\,\,2;\,\, - \,2)\).
Áp dụng công thức:
\(cos((\alpha ),\,(\beta ))\,\, = \,\,\left| {cos(\overrightarrow {{n_\alpha }} ,\,\,\overrightarrow {{n_\beta }} )} \right|\,\, = \,\,\frac{{\left| {\overrightarrow {{n_\alpha }} .\,\,\overrightarrow {{n_\beta }} } \right|}}{{\left| {\overrightarrow {{n_\alpha }} } \right|.\,\,\left| {\overrightarrow {{n_\beta }} } \right|}} = \,\,\frac{{\left| {2.1 - 1.2 - 2.2} \right|}}{{\sqrt {{2^2} + \,\,{{( - 1)}^2}\,\, + \,\,{2^2}} .\sqrt {({1^2}\,\, + \,\,{2^2}\,\, + \,\,{{( - 2)}^2}} }}\,\, = \,\,\frac{4}{9}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
Mặt phẳng \[(P)\], \[(Q)\] có vectơ pháp tuyến lần lượt là \[{\vec n_p} = \left( {m + 2;2m; - m} \right)\], \[{\vec n_Q} = \left( {m;m - 3;2} \right)\]
\[(P) \bot (Q) \Leftrightarrow {\vec n_p}.{\vec n_Q} = 0 \Leftrightarrow \left( {m + 2} \right)m + 2m\left( {m - 3} \right) - 2m = 0 \Leftrightarrow 3{m^2} - 6m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 6\end{array} \right.\]
Câu 2
A. 600
B. 300
C. \[\arcsin \frac{{\sqrt 3 }}{4}\].
D. \[\arccos \frac{{\sqrt 3 }}{4}\].
Lời giải
Chọn D
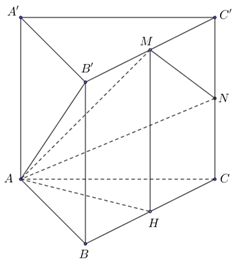
Gọi \[H\] là trung điểm \[BC\], \[BC = a\sqrt 3 \], \[AH = \frac{a}{2}\].
Chọn hệ trục tọa độ \[H\left( {0;0;0} \right)\], \[A\left( {\frac{a}{2};0;0} \right)\], \[B\left( {0;\frac{{a\sqrt 3 }}{2};0} \right)\], \[C\left( {0; - \frac{{a\sqrt 3 }}{2};0} \right)\],
\[M\left( {0;0;a} \right)\], \[N\left( {0; - \frac{{a\sqrt 3 }}{2};\frac{a}{2}} \right)\]. Gọi \[\varphi \] là góc giữa mặt phẳng\(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right)\).
\(\left( {AMN} \right)\) có một vtpt \[\vec n = \left[ {\overrightarrow {AM} ,\overrightarrow {AN} } \right]\]\[ = \left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{4};\frac{{\sqrt 3 }}{4}} \right)\]
\(\left( {ABC} \right)\) có một vtpt \[\overrightarrow {HM} \]\[ = \left( {0;0;1} \right)\], từ đó \[\cos \varphi = \frac{{\left| {\vec n.\overrightarrow {HM} } \right|}}{{\left| {\vec n} \right|HM}}\]\[ = \frac{{\frac{{\sqrt 3 }}{4}}}{{1.1}}\]\[ = \frac{{\sqrt 3 }}{4}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\cos \alpha = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
B.\(\cos \alpha \,\, = \,\,\frac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
C. \[\cos \alpha \,\, = \,\,\frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {CD} } \right]} \right|}}.\]
D.\(\cos \alpha \,\, = \,\,\frac{{\left| {\left[ {\overrightarrow {AB} .\overrightarrow {CD} } \right]} \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\cos \alpha = \frac{1}{{\sqrt 3 }}\).
B. \(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
C. \(\cos \alpha = \frac{1}{{\sqrt {10} }}\).
D. \(\cos \alpha = \frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập