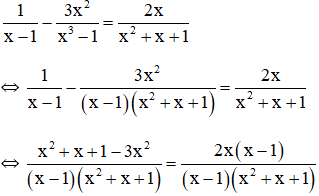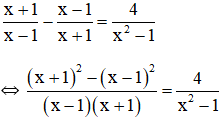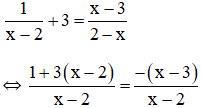Câu hỏi trong đề: Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Quảng cáo
Trả lời:
+ Tìm điều kiện xác định :
x2 + x + 1 = (x2 + x + ¼) + ¾ = (x + ½)2 + ¾ > 0 với mọi x ∈ R.
Do đó x2 + x + 1 ≠ 0 với mọi x ∈ R.
x3 – 1 ≠ 0 ⇔ (x – 1)(x2 + x + 1) ≠ 0 ⇔ x – 1 ≠ 0 ⇔ x ≠ 1.
Vậy điều kiện xác định của phương trình là x ≠ 1.
+ Giải phương trình:
⇒ x2 + x + 1 – 3x2 = 2x(x – 1)
⇔ -2x2 + x + 1 = 2x2 – 2x
⇔ - 4x2 + 3x + 1 = 0
⇔ - 4x2 + 4x - x + 1 = 0
⇔ - 4x(x – 1) – ( x – 1) = 0
⇔ (- 4x - 1)(x – 1) = 0
⇔ - 4x - 1 = 0 hoặc x – 1 = 0
+) Nếu - 4x - 1 = 0 ⇔ - 4x = 1 ⇔ x = -1/4 (thỏa mãn đkxđ)
+) Nếu x – 1 = 0 ⇔ x = 1 (không thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm S = {-1/4}.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện xác định: x ≠ ±1.
Suy ra: x2 + 2x + 1 – (x2 – 2x + 1) = 4
⇔ x2 + 2x + 1 – x2 + 2x – 1 = 4
⇔ 4x = 4
⇔ x = 1 (không thỏa mãn đkxđ)
Vậy phương trình vô nghiệm.
Lời giải
Điều kiện xác định: x ≠ 2.
Suy ra: 1 + 3(x – 2) = -(x – 3)
⇔ 1 + 3x – 6 = -x + 3
⇔ 3x + x = 3 + 6 – 1
⇔ 4x = 8
⇔ x = 2 (không thỏa mãn đkxđ).
Vậy phương trình vô nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.