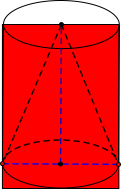
Từ một khúc gỗ hình trụ cao \[24{\mkern 1mu} cm\], người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là \[960\pi {\mkern 1mu} {\mkern 1mu} c{m^3}\]. Tính diện tích xung quanh của hình nón.
Câu hỏi trong đề: 50 bài tập Hình khối trong thực tiễn có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
Ta có \[{V_t} = \pi {R^2}h = 1440\pi \Leftrightarrow \pi {R^2}.24 = 1440\pi \Rightarrow R = 2\sqrt {15} {\mkern 1mu} cm\] nên bán kính đáy của hình nón là \[R = 2\sqrt {15} {\mkern 1mu} cm\], chiều cao hình nón \[h = 24{\mkern 1mu} cm \Rightarrow \] đường sinh hình nón \[{l^2} = {h^2} + {R^2}\] \[ \Rightarrow l = 2\sqrt {159} {\mkern 1mu} cm\]
Diện tích xung quanh hình nón là \[S = \pi Rl = \pi .2\sqrt {15} .2\sqrt {159} = 4\sqrt {2385} \pi {\mkern 1mu} (c{m^2})\]
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
Từ giả thiết ta có \[4\pi {R^2} = 2.\frac{4}{3}\pi {R^3} \Rightarrow {R^3} = \frac{3}{2}{R^2} \Rightarrow R = \frac{3}{2}\]
Lời giải
Chọn D
Gọi \[h\] và \[l\] theo thứ tự là chiều cao và đường sinh của hình nón. Khi đó:
Diện tích xung quanh của hình nón là \(\pi rl\).
Diện tích đáy của hình nón là \(\pi {r^2}\).
Vì hình nón có diện tích xung quanh gấp đôi diện tích đáy nên \(\pi rl = 2\pi {r^2} \Rightarrow l = 2r\).
Lại có \({l^2} = {h^2} + {r^2} \Rightarrow {h^2} = {l^2} - {r^2} = {\left( {2r} \right)^2} - {r^2} = 3{r^2} \Rightarrow h = r\sqrt 3 \).
Vậy thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {r^2}.r\sqrt 3 = \frac{{\sqrt 3 }}{3}\pi {r^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo