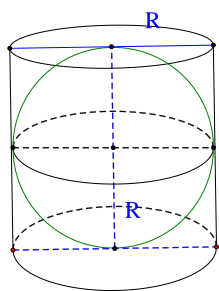
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy và bán kính đáy của hình trụ bằng bán kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
A. \[\frac{4}{3}\].
B. \[\frac{4}{9}\].
C. \[\frac{9}{4}\].
D. \[2\].
Câu hỏi trong đề: 50 bài tập Hình khối trong thực tiễn có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Từ đề bài suy ra chiều cao hình trụ là \[h = 3R\] với \[R\] là bán kính hình cầu và cũng là bán kính đáy của hình trụ.
Thể tích hình cầu \[{V_c} = \frac{4}{3}\pi {R^3}\]; thể tích khối trụ \[{V_t} = \pi {R^2}.3R = 3\pi {R^3}\]
Tỉ số thể tích hình cầu và thể tích hình trụ là \[\frac{{{V_c}}}{{{V_t}}} = \frac{{\frac{4}{3}\pi {R^3}}}{{3\pi {R^3}}} = \frac{4}{9}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(763\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
B. \(679\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
C. \(170\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
D. \(254\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Lời giải
Chọn A
Thể tích của viên đá bằng thể tích của một hình trụ có đường kính đáy bằng \(18cm\), chiều cao bằng \(18 - 15 = 3\,\left( {{\rm{cm}}} \right)\).
Vậy thể tích của viên đá là \(V = \pi {r^2}h = \pi {.9^2}.3 \approx 763\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Câu 2
A. \[7{\mkern 1mu} cm\].
B. \[5{\mkern 1mu} cm\].
C. \[3{\mkern 1mu} cm\].
D. \[9{\mkern 1mu} cm\].
Lời giải
Chọn C
Từ giả thiết ta có \[2\pi Rh + 2\pi {R^2} = 2.2.\pi Rh \Rightarrow Rh = {R^2} \Rightarrow R = h\]
Vậy chiều cao của hình trụ là \[3{\mkern 1mu} \,cm\].
Câu 3
A. \(3\).
B. \(6\).
C. \(9\).
D. \(\frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(40\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
B. \(80\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
C. \(40\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
D. \(80\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[70\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
B. \[80\pi {\mkern 1mu} (c{m^3})\].
C. \[60\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
D. \[10\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{1}{3}\pi {r^3}\).
B. \(\frac{2}{3}\pi {r^3}\).
C. \(\sqrt 3 \pi {r^3}\).
D. \(\frac{{\sqrt 3 }}{3}\pi {r^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(1cm\).
B. \(\frac{{15}}{8}cm\).
C. \(3cm\).
D. \(15cm\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập