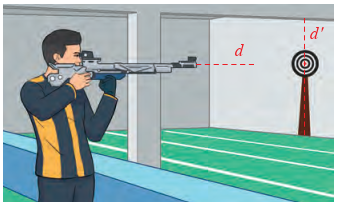
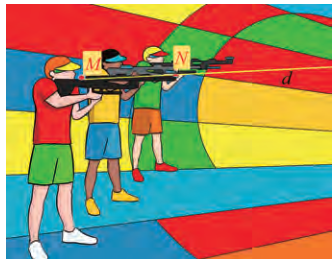
(H.vẽ) Xét tình huống sau:
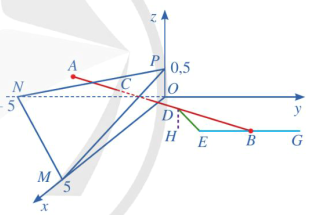
Trong không gian Oxyz , mắt một người quan sát ở điếm \({\rm{M}}(2\); 3; -4) và vật cần quan sát đặt tại điếm \({\rm{N}}( - 1;0;8)\). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm \({\rm{O}}(0;0;0)\), bán kính bằng 3 và đặt trong mặt phắng Oxy .
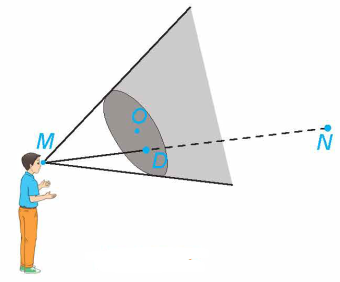
a) Viết phương trình tham số của đường thẳng MN
b) Tính tọa độ giao điểm D của đường thẳng MN với mặt phẳng (Oxy) .
c) Hỏi điểm D có nằm giữa hai điểm \(M\) và \(N\) hay không?
(H.vẽ) Xét tình huống sau:
Trong không gian Oxyz , mắt một người quan sát ở điếm \({\rm{M}}(2\); 3; -4) và vật cần quan sát đặt tại điếm \({\rm{N}}( - 1;0;8)\). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm \({\rm{O}}(0;0;0)\), bán kính bằng 3 và đặt trong mặt phắng Oxy .
a) Viết phương trình tham số của đường thẳng MN
b) Tính tọa độ giao điểm D của đường thẳng MN với mặt phẳng (Oxy) .
c) Hỏi điểm D có nằm giữa hai điểm \(M\) và \(N\) hay không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có \(\overrightarrow {MN} = ( - 3; - 3;12) = - 3(1;1; - 4)\)
Đường thắng MN đi qua điếm \({\rm{M}}(2;3; - 4)\) và có VTCP \(\vec u = (1;1; - 4)\) có phương trình là: \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + t}\\{y = 3 + t}\\{z = - 4 - 4t}\end{array}} \right.\)
b) Mặt phắng Oxy có phương trình là \({\rm{z}} = 0\).
Vi D là giao điếm của đường thắng MN với mặt phắng Oxy nên tọa độ điếm D là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + t}\\{y = 3 + t}\\{z = - 4 - 4t}\\{z = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 2}\\{z = 0}\\{t = - 1}\end{array}} \right.} \right.\).Vậy \(D(1;2;0)\).
c) Ta có \(MD = \sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {{( - 4)}^2}} = \sqrt {18} ;MN = \sqrt {{{( - 3)}^2} + {{( - 3)}^2} + {{12}^2}} = \sqrt {162} \) Vi \({\rm{MD}} < {\rm{MN}}\) nên D nằm giữa M và N .
Vậy tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điếm N .
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
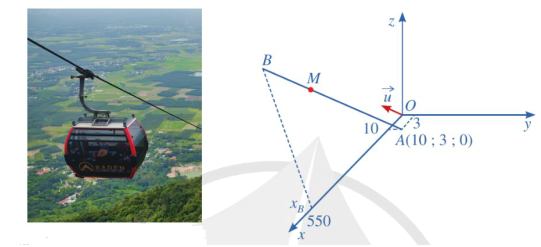
a) Phương trình chính tắc của đường cáp là: \(\frac{{x - 10}}{2} = \frac{{y - 3}}{{ - 2}} = \frac{z}{1}\).
b) Do tốc độ chuyển động của cabin là \(4,5\;{\rm{m}}/{\rm{s}}\) nên độ dài AM bằng \(4,5t(\;{\rm{m}})\). Vì vậy \(|\overrightarrow {AM} | = 4,5t(t \ge 0)\).
Do hai vectơ \(\overrightarrow {AM} \) và \(\vec u\) là cùng phương và cùng hướng nên \(\overrightarrow {AM} = k\vec u\) với \(k\) là số thực dương nào đó. Suy ra: \(|\overrightarrow {AM} | = k|\vec u| = k \cdot \sqrt {{2^2} + {{( - 2)}^2} + 1} = 3k\). Do đó \(3k = 4,5t\). Suy ra \(k = \frac{{3t}}{2}\). Vì thế, ta có: \(\overrightarrow {AM} = \frac{{3t}}{2}\vec u = \left( {3t; - 3t;\frac{{3t}}{2}} \right)\).
Gọi toạ độ của điểm \(M\) là \(\left( {{x_M};{y_M};{z_M}} \right)\).
Do \(\overrightarrow {AM} = \left( {{x_M} - {x_A};{y_M} - {y_A};{z_M} - {z_A}} \right) = \left( {3t; - 3t;\frac{{3t}}{2}} \right)\) nên \(\left\{ {\begin{array}{*{20}{l}}{{x_M} = 3t + {x_A}}\\{{y_M} = - 3t + {y_A}}\\{{z_M} = \frac{{3t}}{2} + {z_A}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_M} = 3t + 10}\\{{y_M} = - 3t + 3}\\{{z_M} = \frac{{3t}}{2}.}\end{array}} \right.} \right.\)
Vậy điểm \(M\) có toạ độ là \(\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).
c) Do \({x_B} = 550\) nên \(3t + 10 = 550\), tức là \(t = 180\) (s). Do đó, ta có điểm \(B(550; - 537;270)\).
Vậy \(AB = \sqrt {{{(550 - 10)}^2} + {{( - 537 - 3)}^2} + {{(270 - 0)}^2}} = \sqrt {656100} = 810(\;{\rm{m}})\).
d) Đường thẳng AB có vectơ chỉ phương \(\vec u = (2; - 2;1)\) và mặt phẳng (Oxy) có vectơ pháp tuyếnDo đó, ta có: Vậy
Lời giải
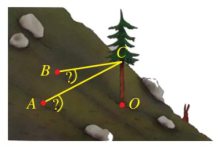
a) Do điểm \(C(0;0;5)\) nên \(AC = \sqrt {{{(3 - 0)}^2} + {{( - 4 - 0)}^2} + {{(2 - 5)}^2}} = \sqrt {34} (\;{\rm{m}})\);
\(BC = \sqrt {{{( - 5 - 0)}^2} + {{( - 2 - 0)}^2} + {{(1 - 5)}^2}} = \sqrt {45} = 3\sqrt 5 (\;{\rm{m}}){\rm{. }}\)
b) Ta có: \(\overrightarrow {OA} = (3; - 4;2),\overrightarrow {OB} = ( - 5; - 2;1)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{l}}{ - 4}&2\\{ - 2}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&{ - 4}\\{ - 5}&{ - 2}\end{array}} \right|} \right) = (0; - 13; - 26){\rm{. }}\)
Vì thế, vectơ \(\vec n = (0;1;2)\) là một vectơ pháp tuyến của mặt phẳng \((OAB)\).
Mặt khác, do \(\overrightarrow {CA} = (3; - 4; - 3),\overrightarrow {BC} = (5;2;4)\) nên ta có:
- \(\sin (CA,(OAB)) = |\cos (\overrightarrow {CA} ,\vec n)| = \frac{{|\overrightarrow {CA} \cdot \vec n|}}{{|\overrightarrow {CA} | \cdot |\vec n|}} = \frac{{|3 \cdot 0 + ( - 4) \cdot 1 + ( - 3) \cdot 2|}}{{\sqrt {34} \cdot \sqrt 5 }} = \frac{{10}}{{\sqrt {170} }}\),
suy ra . Vậy góc tạo bởi dây neo CA và mặt phẳng sườn núi là khoảng .
suy ra . Vậy góc tạo bởi dây neo BC và mặt phẳng sườn núi là khoảng .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập